
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение. Удельное сопротивление проводников (при 00 С), мкОм × м Алюминий Графит Железо
| Воск Вода Керосин Масло | 7,8 | Парафин слюда Стекло Фарфор | Эбонит Парафинированная бумага | 2,6 |
Удельное сопротивление проводников (при 00 С), мкОм × м
| Алюминий Графит Железо Медь | 0,025 0.039 0,087 0.017 | Нихром Ртуть Свинец Сталь | 0,94 0,22 0.10 |
Масса покоя некоторых частиц
| Частица | m0 | |
| кг | а.е.м. | |
| Электрон Протон Нейтрон Дейтрон a - частица | 9,11 10-31 1,672 10-27 1,675 10-27 3,35 10-27 6,64 10-27 | 0,00055 1,00728 1,00867 2,01355 4,00149 |
ЭЛЕКТРИЧЕСТВО, МАГНЕТИЗМ, ЭЛЕКТРОМАГНЕТИЗМ, ОПТИКА
Часть II
Руководство к лабораторным работам по физике
для студентов специальности «Лечебное дело»
Под редакцией Р.Н. Ростовцева
С.Е. Кажарской
О.В. Шуваевой
Тула
Издательство ТулГУ
УДК
Электричество, магнетизм, электромагнетизм, оптика. Часть II. Руководство к лабораторным работам по физике для студентов специальности «Лечебное дело» / под ред. Р.Н. Ростовцева, С.Е. Кажарской, О.В. Шуваевой. Тула: Изд-во ТулГУ, 2011. 82 с.
ISBN 987–5–7679–1851–5
Данное учебно-методическое пособие содержит лабораторные работы по физике, которые будут предложены студентам первого курса специальности «Лечебное дело» в весеннем семестре.
Каждая лабораторная работа содержит краткое теоретическое введение с основными понятиями, формулами, формулировками законов, необходимыми для выполнения лабораторной работы и подготовки к ее защите.
Табл.15. Илл. 44. Библиогр.: 4 назв.
Печатается по решению библиотечно-издательского совета Тульского государственного университета
Рецензент: д-р техн. наук, проф. Чуканов А.Н.
Ó Ростовцев Р.Н., Кажарская С.Е.,
Шуваева О.В., 2011
Ó Изд-во ТулГУ, 2011
ISBN 987–5–7679–1851–5
ЛАБОРАТОРНАЯ РАБОТА 10
ИССЛЕДОВАНИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Цель работы:экспериментальное исследование зависимостиполной и полезной мощностей от отношения сопротивлений нагрузки и источника. Изучение мостовых схем и проверка справедливости закона Ома.
Приборы и принадлежности:источник постоянного питания, измерительное устройство с вольтметром и миллиамперметром, набор резисторов и монтажных проводов.
Теоретическое введение
Воздействие постоянного тока на организм зависит от силы тока, поэтому весьма существенную роль играет электрическое сопротивление тканей и прежде всего кожи. В медицине используют постоянный электрический ток для лечебных и диагностических целей.
Электрофорез – это метод, основанный на введении лекарственного средства через кожу или слизистые оболочки под действием постоянного тока.
Гальванизация — физиотерапевтический метод, основанный на пропускании через ткани организма постоянного тока под напряжением 60–80 В.
При гальванизации различных участков тела используют следующие различные токи:
конечности — 20–30 мА,
туловище — 15–20 мА,
части лица — 3–5 мА,
слизистые оболочки — 2–3 мА.
При проведении гальванизации в подлежащих тканях активизируются системы регуляции локального кровотока. Происходит расширение просвета дермальных сосудов и возникает гиперемия кожных покровов. Расширение капилляров и повышение проницаемости их стенок происходит не только в месте приложения электродов, но и в глубоко расположенных тканях, через которые проходит постоянный электрический ток.
Электропроводность тканей и органов зависит от функционального состояния и может быть использована как диагностический фактор.
Введем основные понятия и законы теории электричества.
Сила тока I равна заряду, протекающему через поперечное сечение проводника (перпендикулярное вектору 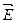 ) за единицу времени:
) за единицу времени:  . Сила тока измеряется в амперах.
. Сила тока измеряется в амперах.
Ток, текущий по проводнику, удовлетворяет закону Ома для участка цепи:
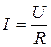 , (1)
, (1)
где U – напряжение на проводнике, R – сопротивление проводника. Опыт показывает, что сопротивление проводника зависит от его формы, размеров и материала, из которого изготовлен проводник. Сопротивление однородного цилиндрического проводника может быть рассчитано по формуле
 , (2)
, (2)
где 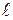 – длина проводника; S – площадь поперечного сечения;
– длина проводника; S – площадь поперечного сечения;  – величина, зависящая от материала проводника, называемая удельным сопротивлением материала:
– величина, зависящая от материала проводника, называемая удельным сопротивлением материала:  .
.
Таким образом, удельное сопротивление численно равно сопротивлению проводника, имеющего длину 1 м и площадь поперечного сечения 1 м2. В системе СИ единицей измерения  является 1 Ом×м.
является 1 Ом×м.
Кроме удельного сопротивления  используют также обратную величину
используют также обратную величину 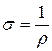 , называемую удельной проводимостью или удельной электропроводностью.
, называемую удельной проводимостью или удельной электропроводностью.
Если проводник имеет произвольную форму или клеммы, через которые к нему подводят напряжение, расположены в произвольных точках его поверхности, то сопротивление этого проводника, определяемое законом Ома, сохраняет свой смысл, но его уже нельзя вычислить при помощи формулы (2) . Плотность тока  будет различной в разных точках проводника. Поэтому распределение плотности тока в объеме проводника следует определять, используя фундаментальное соотношение
будет различной в разных точках проводника. Поэтому распределение плотности тока в объеме проводника следует определять, используя фундаментальное соотношение
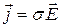 , (3)
, (3)
называемое законом Ома в локальной форме. (  – вектор напряженности электрического поля в данной точке проводника).
– вектор напряженности электрического поля в данной точке проводника).
Физическое содержание понятий удельного сопротивления и удельной проводимости можно понять, исходя из представлений классической электронной теории. В этой теории предполагают, что свободные электроны в металлах ведут себя подобно идеальному газу. Если в проводнике создать электрическое поле  , то на хаотическое тепловое движение электронов, которому соответствует средняя скорость
, то на хаотическое тепловое движение электронов, которому соответствует средняя скорость 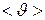 , наложится упорядоченное движение со средней скоростью
, наложится упорядоченное движение со средней скоростью  – скоростью дрейфа. При этом
– скоростью дрейфа. При этом
 , (4)
, (4)
где n – число электронов в единице объема; е – заряд электрона. Предполагается, что максимальное значение направленной составляющей скорости 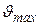 , которую приобретает электрон между двумя последовательными столкновениями с ионами кристаллической решетки, полностью теряется при столкновении. При этом энергия упорядоченного движения электронов преобразуется во внутреннюю энергию проводника, который нагревается при прохождении по нему электрического тока. Вычисления приводят к следующему выражению для средней скорости направленного движения электронов
, которую приобретает электрон между двумя последовательными столкновениями с ионами кристаллической решетки, полностью теряется при столкновении. При этом энергия упорядоченного движения электронов преобразуется во внутреннюю энергию проводника, который нагревается при прохождении по нему электрического тока. Вычисления приводят к следующему выражению для средней скорости направленного движения электронов  , (5)
, (5)
где  – средняя длина свободного пробега электронов, которую считают по порядку величины равной параметру кристаллической решетки материала; т – масса электрона. Подставляя формулу (5) в (6), получаем
– средняя длина свободного пробега электронов, которую считают по порядку величины равной параметру кристаллической решетки материала; т – масса электрона. Подставляя формулу (5) в (6), получаем  , что при сопоставлении с законом Ома в локальной форме дает для удельной проводимости выражение
, что при сопоставлении с законом Ома в локальной форме дает для удельной проводимости выражение 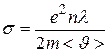 .
.
Данная лабораторная работа ставит своей целью исследовать цепь постоянного тока (задание 1), а также сопротивления и проверить выполнимость закона Ома (задание 2).
Источник ЭДС Е с внутренним сопротивлением r, нагруженный на внешнее сопротивление R , создает в цепи ток  . Мощность Р=ЕI, развиваемая источником, делится между нагрузкой
. Мощность Р=ЕI, развиваемая источником, делится между нагрузкой  и источником
и источником 
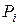 в том же отношении , что и напряжение:
в том же отношении , что и напряжение:
 ;
;  . (6)
. (6)
Мощность  , выделяющуюся в нагрузке, называют полезной. Отношение
, выделяющуюся в нагрузке, называют полезной. Отношение  – коэффициент полезного действия источника.
– коэффициент полезного действия источника.
С увеличением внешнего сопротивления от нуля (короткое замыкание) до бесконечности (разомкнутая цепь) напряжение на нагрузке растет от нуля до значения равного ЭДС, а ток в цепи уменьшается от  при коротком замыкании до нуля при разомкнутой цепи. Максимальное значение полезной мощности достигается при согласовании сопротивлений источника и нагрузки: R = r,
при коротком замыкании до нуля при разомкнутой цепи. Максимальное значение полезной мощности достигается при согласовании сопротивлений источника и нагрузки: R = r,
 . (7)
. (7)
Полная мощность Р с увеличением сопротивления нагрузки уменьшается и в режиме согласования составляет 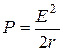 – это половина мощности, развиваемой источником в режиме короткого замыкания:
– это половина мощности, развиваемой источником в режиме короткого замыкания:
 . (8)
. (8)
Внешнее напряжение источника в режиме согласования равно половине ЭДС; КПД источника в этом режиме составляет 0,5.
Для определения сопротивления проводников существуют различные методы. Одним из них является метод измерения сопротивлений при помощи мостовой схемы. Мостовые схемы представляют собой разветвленные цепи, для которых применяются правила Кирхгофа.
Первое правило Кирхгофа гласит, что алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
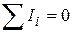 . (9)
. (9)
Это уравнение можно написать для каждого из N узлов цепи, однако, независимыми являются только (N – 1) уравнение. Направления токов в участках цепи выбирают произвольно, а знаки для определенности считают положительными для токов, подходящих к узлу, и отрицательными для токов, отходящих от узла.
Второе правило Кирхгофа гласит, что алгебраическая сумма напряжений в замкнутом контуре равна алгебраической сумме ЭДС, входящих в этот контур:
 . (10)
. (10)
При заданном направлении обхода контуров положительными считаются те токи и ЭДС, направления которых совпадают с направлением обхода. Среди уравнений (10) независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров друг на друга.
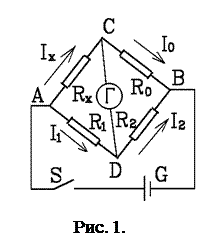 Мостовая схема постоянного тока, часто называемая сокращенно мостом Уитстона, представляет собой замкнутый четырехуголник, составленный из сопротивлений
Мостовая схема постоянного тока, часто называемая сокращенно мостом Уитстона, представляет собой замкнутый четырехуголник, составленный из сопротивлений  (рис. 1). В диагональ АВ четырехугольника включается источник постоянного тока с электродвижущей силой
(рис. 1). В диагональ АВ четырехугольника включается источник постоянного тока с электродвижущей силой  , в диагональ СD – чувствительный гальванометр Г. Эта диагональ схемы и называется мостом в собственном смысле. Весь процесс измерений при помощи этой схемы связан с требованием равенства нулю тока в мосте, отсюда и распространение названия “мост” на всю схему. При произвольном соотношении сопротивлений, составляющих всю мостовую схему, через гальванометр, разумеется, должен идти ток, но существует одно определенное соотношение между сопротивлениями, при котором ток, идущий через гальванометр, обращается в нуль, хотя при этом во всех других звеньях схемы ток не равен нулю.
, в диагональ СD – чувствительный гальванометр Г. Эта диагональ схемы и называется мостом в собственном смысле. Весь процесс измерений при помощи этой схемы связан с требованием равенства нулю тока в мосте, отсюда и распространение названия “мост” на всю схему. При произвольном соотношении сопротивлений, составляющих всю мостовую схему, через гальванометр, разумеется, должен идти ток, но существует одно определенное соотношение между сопротивлениями, при котором ток, идущий через гальванометр, обращается в нуль, хотя при этом во всех других звеньях схемы ток не равен нулю.
Если ток в гальванометре отсутствует, то применяя к контурам ADCA и CBDC второе правило Кирхгофа получим
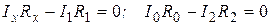 . (11)
. (11)
Применяя к узлам С и D первое правило Кирхгофа, будем иметь
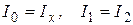 . (12)
. (12)
Из этих выражений следует
 или
или 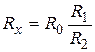 . (13)
. (13)
Сопротивлением  обычно служит магазин сопротивлений. Сопротивлениями
обычно служит магазин сопротивлений. Сопротивлениями  и
и 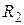 служат части реохорда АВ. Реохордом называют однородную проволоку, изготовляемую из высокоомного материала. По проволоке реохорда перемещается подвижный контакт D, соединенный с гальванометром Г. Вследствие того, что проволока реохорда однородна и тщательно калибрована, отношение сопротивлений участков цепи AD и DB (плеч реохорда) на основании формулы (5) можно заменить отношением соответствующих длин плеч реохорда
служат части реохорда АВ. Реохордом называют однородную проволоку, изготовляемую из высокоомного материала. По проволоке реохорда перемещается подвижный контакт D, соединенный с гальванометром Г. Вследствие того, что проволока реохорда однородна и тщательно калибрована, отношение сопротивлений участков цепи AD и DB (плеч реохорда) на основании формулы (5) можно заменить отношением соответствующих длин плеч реохорда
 . (14)
. (14)
Дата добавления: 2014-10-31; просмотров: 374; Мы поможем в написании вашей работы!; Нарушение авторских прав |