Теоретическое введение. Живой организм представляет собой систему колебательных структур различной природы

Живой организм представляет собой систему колебательных структур различной природы. Способы описания колебаний одинаковы для любых процессов. Поэтому исследуем колебания в колебательном контуре. В теоретическом введении лабораторной работы 11 описаны свободные колебания (затухающие), возникающие в электрическом колебательном контуре.

Чтобы в реальной колебательной системе (содержащей сопротивление) получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью подключения к контуру переменного напряжения. Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, ЭДС которого изменяется по гармоническому закону:

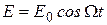. (1)

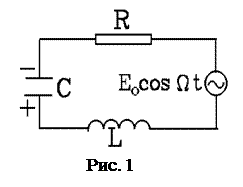
В любой момент времени сумма падений напряжения на элементах цепи равна ЭДС (рис.1):

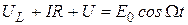. (2)

Падение напряжения на катушке индуктивностью L (равное ЭДС индукции)

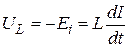, (3)

ток в катушке и в контуре

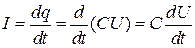. (4)

Подставляем (3) и (4) в (2) , вводим обозначения 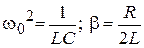, (5)

где 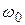– собственная частота контура, 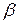– коэффициент затухания.

Получаем дифференциальное уравнение второго порядка

. (6)

Его решение дает закон изменения напряжения на конденсаторе с течением времени. Установившиеся колебания в цепи происходят с частотой 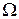и возможным сдвигом по фазе. Поэтому решение ищут в виде

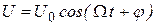, (7) где амплитуда напряжения 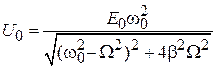; (8)

сдвиг фаз 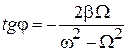. (9)

Таким образом, амплитуда и фаза напряжения на конденсаторе зависят от соотношения частоты источника ЭДС 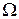и собственной частоты контура .

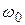Ток в контуре тоже меняется по гармоническому закону, амплитуда тока в контуре так же зависит от соотношения 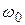и :

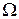. (10)

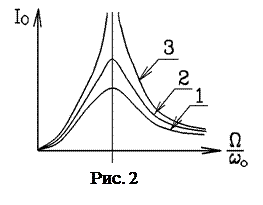
График зависимости 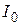от представлен на рис. 2.

Из графика видно, что амплитуда тока резко возрастает при приближении циклической частоты источника ЭДС 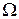к частоте 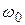. Это явление называется резонансом, а кривые – резонансными кривыми. Величина максимума зависит от 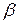: при 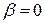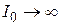(кривая 3); при увеличении 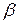максимальное значение амплитуды тока уменьшается (кривые 2 и 1), 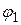определяет разность фаз колебаний тока в контуре и внешней ЭДС.

Резонанс напряжений наступает, если частота источника

. (11)

При b² << w² значение резонансной частоты практически совпадает с собственной.

Коэффициент затухания биологических систем достаточно велик. Если бы коэффициент затухания был мал, то резонансные явления, возникающие во внутренних органах человека под воздействием внешних вибраций, могли бы привести к разрыву органов, повреждению связок и т.п.

Одной из характеристик колебательного контура является добротность 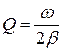, где 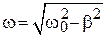. (По определению ).

Добротность контура связана с остротой резонансных кривых. Ширину резонансной кривой измеряют на высоте (рис. 3) .

Если известны параметры контура, добротность может быть рассчитана по соотношению

. (12)

Последнее выражение можно преобразовать

. (13)

Таким образом, добротность контура показывает, во сколько раз максимальное значение амплитуды напряжения на конденсаторе (и на индуктивности) превышает амплитуду внешней ЭДС.

Резонанс используют для выделения из сложного напряжения нужной составляющей. На этом основана техника радиоприема. Для того, чтобы радиоприемник принимал интересующую нас радиостанцию, его необходимо настроить, т.е. изменением L и C колебательного контура добиться совпадения его собственной частоты с частотой электромагнитных волн, излучаемых радиостанцией. Чем меньше затухание, т.е. чем выше добротность, тем сильнее возрастает амплитуда в точке резонанса и тем уже и выше становится пик амплитудно-частотной характеристики. Принято считать, что контур усиливает сигналы тех частот, для которых амплитуды отличаются от резонансного значения не больше, чем в 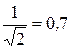раз. Интервал таких частот 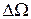называется полушириной резонанса.

Из формулы (13) следует, что добротность 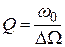, т. е. чем меньше добротность контура, тем больший интервал частот 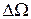он будет усиливать, а чем больше добротность, тем больше избирательная способность контура усиливать при настройке только очень узкий интервал частот (соответствующий определенной радиостанции).