Теоретическое введение. Исходя из представлений о колебательном характере всех процессов в живых системах, предполагается, что живой организм есть сложно организованная система

Исходя из представлений о колебательном характере всех процессов в живых системах, предполагается, что живой организм есть сложно организованная система колебательных структур (осцилляторов) различной природы. Таким образом, биологический объект представляет собой совокупность колебательных цепей. Различные по природе колебательные процессы имеют одинаковые характеристики и описываются одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы.

В замкнутой электрической цепи, содержащей катушку индуктивности L и конденсатор С, могут возникнуть электромагнитные колебания. Поэтому такую цепь называют колебательным контуром. Если к электрическому контуру не подключены внешние источники переменной ЭДС, то колебания называются собственными. Иначе говоря, свободными (собственными) колебаниями называют такие колебания, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.

Если зарядить конденсатор от батареи до напряжения (рис. 1), а затем повернуть переключатель К, то конденсатор начнет разряжаться через катушку и в контуре возникнут электромагнитные колебания. Рассмотрим, как происходят эти колебания в контуре, сопротивление которого R = 0 . При замыкании контура в нем появляется ток I , создающий магнитное поле.

Возрастание тока ведет к возрастанию индукции магнитного поля катушки и, следовательно, к увеличению магнитного потока, пронизывающего катушку (соленоид). При всяком изменении магнитного потока, пронизывающего замкнутый контур, в этом контуре возникает ЭДС индукции (в нашем случае речь идет о ЭДС самоиндукции). Возникшая стремится скомпенсировать увеличение магнитного потока, что приводит к замедлению процесса разрядки конденсатора. В момент, когда конденсатор полностью разрядится, ток в цепи не прекращается сразу, а продолжает течь в том же направлении и, постепенно затухая, перезаряжает конденсатор (рис. 2). Затем процесс разрядки начинается снова, но теперь протекает в обратном направлении. В результате вторичной перезарядки конденсатора система возвращается в исходное состояние. Время, за которое происходит возвращение системы в исходное состояние, называется периодом собственных колебаний Т. Период колебаний в таком контуре равен , а частота .

Эта частота называется собственной частотой колебательного контура.

В начальный момент, когда конденсатор полностью заряжен, в нем накоплена электрическая энергия . Во время разрядки конденсатора электрическая энергия превращается в энергию магнитного поля тока, протекающего через катушку индуктивности, и полная энергия будет равна , когда конденсатор полностью разрядится, вся энергия перейдет в магнитную (где 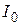– наибольшая (амплитудная) величина тока в контуре). При перезарядке конденсатора энергия магнитного поля снова превратится в энергию электрического поля. В контуре возникают незатухающие электромагнитные колебания (напомним, что сопротивление в контуре считаем равным нулю).

Получим уравнение колебаний в контуре (рис. 5), содержащем активное сопротивление R. По второму закону Кирхгофа можно записать:

. (1)

ЭДС индукции, возникающая в катушке, определяется так: . (2)

Заряд на конденсаторе , а ток

, (3)

тогда из (2) и (3) следует:

; .

Подставив последние выражения в (1), получаем уравнение электрических колебаний в контуре (колебания напряжения на конденсаторе):

. (4)

Как известно, полученное дифференциальное уравнение описывает затухающие колебания. Его решение имеет вид:

, (5)

где 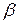– коэффициент затухания, Т – период колебаний, – циклическая частота затухающих колебаний. В этом уравнении амплитуда колебаний меняется со временем (рис. 3).

; (6)

при этом

. (7) Время, за которое амплитуда колебаний уменьшается в е раз называется временем релаксации: .

Из формул (7) следует, что в контуре возможны затухающие колебания лишь в том случае, если , (частота и период – действительные величины).

Сопротивление, определенное из этого условия 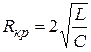(8)

называется критическим.

Если сопротивление в контуре больше критического, то частота и период – мнимые величины. Колебания в таком контуре не возникают, а происходит апериодический разряд конденсатора (рис. 4).

Для характеристики степени затухания колебаний, кроме коэффициента затухания 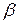используется еще логарифмический декремент затухания.

Логарифмическим декрементом затухания колебаний называется натуральный логарифм отношения двух амплитудных значений напряжения, разделенных интервалом времени, равным периоду колебаний:

или , (9)

где – начальная амплитуда, – амплитуда n-го колебания.

Подставив в (9) значения и 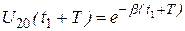, получим

. (10)