Приклад розв'язання задачі

Це завдання вимагає від студента уміння будувати епюри, поздовжніх сил, нормальних напруг і визначити подовження або вкорочення бруса.

При роботі бруса на розтяг і стиск в його поперечних перетинах виникає поздовжня сила N. Поздовжня сила в довільному поперечному перерізі бруса чисельно дорівнює алгебраїчній сумі проекцій на його поздовжню вісь всіх зовнішніх сил, що діють на відсічену частину.

Для розрахунку на міцність і визначення переміщень необхідно знати закон зміни поздовжніх сил по його довжині. Правило знаків: при розтязі поздовжня сила додатна, при стиску - від'ємна. Умова міцності при розтязі і стиску має вигляд 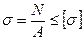, де σ, N - відповідно нормальне напруження і поздовжня сила в небезпечному перерізі (тобто в перерізі, де виникають найбільші напруги); А - площа поперечного перерізу; [σ] - допустима напруга. За умовою міцності можна вирішувати три види завдань:

1) перевірка міцності,

2) підбір перерізу ;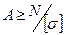

3) визначення допустимої навантаження .

Послідовність виконання завдання:

1. Розбити брус на ділянки, починаючи від вільного кінця. Межами ділянок є перетини, в яких прикладені зовнішні сили, а для напруг також і місця зміни розмірів поперечного перерізу.

2. Визначити за методом перерізів поздовжню силу для кожної ділянки (ординати епюри N;) і побудувати епюру поздовжніх сил N. Провівши паралельно осі бруса базову (нульову) лінію епюри, відкласти перпендикулярно їй в довільному масштабі одержані значення ординат. Через кінці ординат провести лінії, проставити знаки і заштрихувати епюру лініями, паралельно ординатам.

3. Для побудови епюри нормальних напружень визначаємо напруги в поперечних перерізах кожної із ділянок. У межах кожної ділянки напруги постійні, тобто епюра на даній ділянці зображується прямою, паралельною осі бруса.

4. Переміщення вільного кінця бруса визначаємо як суму подовжень (вкорочень) ділянок бруса, обчислених за формулою Гука.

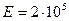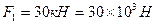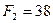Приклад 4. Для даного ступінчатого брусу (рис. 3, а) побудувати епюру поздовжніх сил, епюру нормальних напружень і визначити переміщення вільного кінця, якщо МПа; ; кН; ; ; .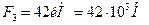

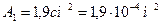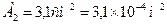Розв'язання:

1. Розбиваємо брус на ділянки, як показано на рис. 3 а.

2. Визначаємо ординати епюри N на ділянках бруса:

; ; ; ; .

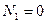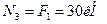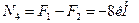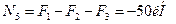Будуємо епюру поздовжніх сил (рис. 3 б).

3. Обчислюємо ординати епюри нормальних напружень:

;

;

;

.

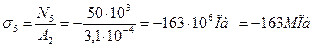Будуємо епюру нормальних напружень (рис. 3, в).

4. Визначаємо переміщення вільного кінця:

;

;

;

;

;

.

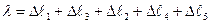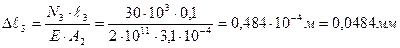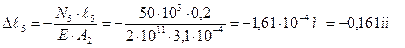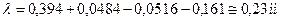Брус подовжується на 0,23 мм.

Питання для самоконтролю

1. В якому випадку переміщення вільного кінця однорідного бруса при осьовій дії зовнішніх сил дорівнює нулю ?

2. В якому випадку переміщення перерізу mn. однорідного
бруса при осьовій дії зовнішніх сил направлено зліва

1. направо ?

2. В якому випадку епюра нормальних сил по довжині однорід­ного бруса при осьовій дії зовнішніх сил має як від’ємні, так і додатні значення ?

3. В якому випадку епюра нормальних напружень по довжині однорідного бруса при осьовій дії зовнішніх сил має тільки додатні значення ?

4. В якому випадку переміщення вільного кінця однорідного бруса при осьовій дії зовнішніх сил найбільше ?