ЛІТЕРАТУРА ДОДАТКОВА. 1. Розрахунки на міцність при деформації “зсув”

1. Розрахунки на міцність при деформації “зсув”

Зсув – це один з простих видів навантаження (деформування) бруса, при якому у поперечному перерізі бруса діє тільки внутрішня поперечна сила ( 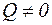). Практичним прикладом такого навантаження є різання ножицями металевих штаб або прутків.

Розглянемо брус, перпендикулярно осі якого прикладені дві рівні протилежно направлені сили , лінії дії котрих паралельні і знаходяться на незначній відстані (рисунок 1 а). При цьому елемент бруса довжиною зазнає деформації зсуву.

Для визначення поперечної сили використовуємо метод перерізів (статична сторона задачі). З умови рівноваги лівої частини бруса (рисунок1 б)

(1)

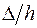З геометричної точки зору зсув характеризується величинами: – абсолютний зсув; – відносний зсув, що є мірою перекосу прямих кутів елемента. При деформації елемента в межах пружності значення 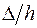дуже мале і його можливо виразити через кут зсуву

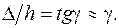(2)

Фізична сторона представлена законом Гука при зсуві:

Дотичні напруження прямо пропорційні кутовим деформаціям.

, (3)

де 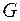- модуль пружності другого роду або модуль зсуву.

Для сталі . Можна довести теоретично, що пружні константи зв’язані між собою такою залежністю:

. (4)

Строго кажучи, задача визначення закону розподілу дотичних напружень 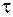по перерізу бруса статично невизначувана і потребує сумісного аналізу з статичної, геометричної та фізичної сторін (рівняння (1) – (3)). Але на практиці замість аналізу точної картини розподілу деформацій і напружень в перерізі приймають досить грубий спрощений підхід: приймають умовний рівномірний розподіл .

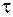Якщо прийнято, що 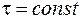, то можна цю величину винести за знак інтеграла в рівнянні (1) і отримати розрахункову формулу

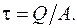(5)

Якщо в формулу закону Гука (3) підставити 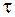і 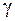, то ми отримаємо формулу для визначення абсолютного зсуву

. (6)

В цій формулі добуток 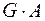називається жорсткістю при зсуві.

Незважаючи на те, що формули (5) і (6) з теоретичної точки зору не досить коректні, але практичні розрахунки на міцність дають надійний результат, бо неточності методу враховуються нормативним коефіцієнтом запасу або величиною допустимого напруження .

Умова міцності при зсуві має вигляд

(7)

Допустиме дотичне напруження при зсуві можливо виразити через допустиме напруження при розтягу .

Питання для самоконтролю

1. Який напружений стан називається чистим зсувом? Навести прик­лади.

2. Навести приклади деталей, які працюють на зріз і зминання.

3. Запищіть закон Гука для зсуву.

4. Що таке умовна площа зминання деталі?

5. Запишіть в загальному вигляді умову міцності при зрізі і при зминанні.