Осьові, полярний і відцентровий моменти інерції

Осьовим моментом інерції плоского перетину щодо даної осі називається взята по всій площі перетину сума добутків площ елементарних площадок на квадрати їхніх відстаней до цієї осі (рис.4).

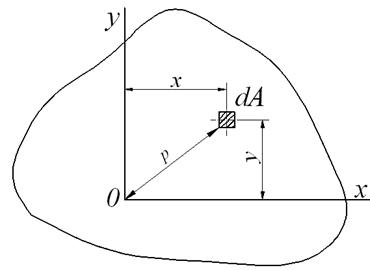
Рис.4. До визначення моментів інерції

Із цього визначення виходить, що момент інерції щодо осі 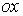являє собою визначений інтеграл

(4)

Аналогічно, момент інерції щодо осі

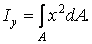
(4')

У технічній літературі ці характеристики іноді називають екваторіальними моментами інерції.

Осьовий момент інерції може бути тільки додатною величиною, тому що незалежно від знака координати довільної площадки відповідний доданок додатній, так як в нього входить квадрат цієї координати. Розмірність осьового моменту інерції — довжина в четвертому ступені (виміряється в м⁴, см⁴,мм⁴).

Якщо положення елементарної площі d визначено радіус- вектором (рис.4), то величину

(5)

називають полярним моментом інерції.

Очевидно, що 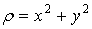(рис.8), тому для будь-якого перетину

.

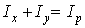(6)

Розмірність цієї величини — м⁴, см⁴, мм⁴.

При визначенні осьових моментів інерції в деяких випадках доводиться зустрічатися ще з однією геометричною характеристикою — відцентровим моментом інерції. Це взята по всій площі перетину сума добутків площ елементарних площадок на добуток їхніх відстаней до двох даних взаємно перпендикулярних осей, тобто

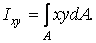
(7)

Відцентровий момент інерції має розмірність довжини в четвертому ступені. Залежно від розташування осей він може бути як додатнім, так і від'ємним і в окремих випадках рівним нулю.