Фазовая плоскость, фазовая траектория. Построение фазовой траектории методом изоклин.

Вопрос

Понятие нелинейной системы (НСАУ).

К нелинейным САУ относят системы, которые не могут быть описаны линейными дифференциальными уравнениями. В большинстве случаев возможно выделить отдельно линейную и нелинейную части (рисунок 9.1):

Нелинейный элемент при этом подчиняется следующим правилам:

1) нелинейный элемент представляет собой безинерционное звено. То есть описывается обыкновенным уравнением;

2) его характеристикой является статическая зависимость сигнала на выходе от сигнала на входе. Например, как на рисунке 9.2:

Примеры нелинейных элементов показаны на рисунке 9.3:

Нарушение принципа суперпозиции в НСАУ.

Построение математического аппарата для линейных систем основано на принципе суперпозиции – реакция системы на сумму воздействий равно сумме реакций системы на каждое воздействие в отдельности. Поэтому пмплитудные и фазовые частотные характеристики не зависят от амплитуды сигналов. В нелинейных системах принцип суперпозиции нарушается. Например, для нелинейностей типа насыщения (рисунок 9.4).

Необходим инструмент, который бы описывал поведение НСАУ с учетом начальных условий (амплитуды сигналов).

Вектор состояний. Пространство состояний. Фазовое пространство. Фазовая плоскость.

Всегда можно выделить такой вектор сигналов x={x₁, x₂, …, x_n}, однозначно определяющий состояние системы. Размерность вектора будет определяться порядком системы (ее характеристического уравнения). Например, для двигателя постоянного тока независимого возбуждения вектором состояний будет являться совокупность сигналов x={I_я, I_в, ω, t⁰}:

а) ток якоря I_я;

б) ток возбуждения I_в;

в) скорость вращения ω;

г) температура двигателя t⁰.

Совокупность всех векторов состояний образуют пространство состояний. Таким образом, в определенное время вектор состояния любой системы имеет конкретные координаты в пределах пространства состояний. С течением времени координаты вектора изменяются, и конец вектора описывает траекторию движения (рисунок 9.5).

Однако с точки зрения управления не все составляющие вектора состояний необходимы. Например, для двигателя постоянного тока в контуре регулирования скорости необходима информация о скорости вращения двигателя. Совокупность необходимых для управления величин образуют вектор управляющих величин.

В то же время порядок вектора состояний (вектора управляющих величин) должен соответствовать порядку уравнения объекта управления. Для одной управляющей величины применяют следующую форму записи вектора состояний:

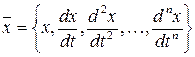
Совокупность таких векторов состояний образует фазовое пространство. А траектория движения в таком пространстве называется фазовой траекторией.

Для систем второго порядка фазовая траектория будет отображаться в фазовой плоскости, по оси абсцисс которой откладывается значение управляемой величины x, а по оси ординат – значение производной x по времени (скорость изменения x).

Свойства фазовой траектории.

Пусть свободное движение системы описывается нелинейным дифференциальным уравнением:

.

Введем дополнительную координату:

, т.е. .

Тогда дифференциальное уравнение можно переписать следующим образом:

.

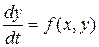Уравнение фазовой траектории выводится из последнего путем перехода в фазовую плоскость с координатами (x,y) – необходимо и правую и левую части разделить на y:

.

Решая получившееся дифференциальное уравнение можно получить уравнение фазовой траектории.

Свойства фазовой траектории:

1) при y>0 (скорость изменения x положительна) траектория движения идет слева на право (x увеличивается), при y<0 траектория движения идет справа на лево;

2) при y=0, . Так как определяет угловой коэффициент касательной к траектории движения, то фазовая траектория пересекает ось x (y=0) под прямым углом (tg 90⁰→∞).

3) конец движения находится на оси x и подчиняется правилам y=0, 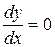. В отличие от точки пересечения оси x фазовая траектория к точке остановки может приближаться под любым углом (согласно правилу 1).

Пример фазовой траектории показан на рисунке 9.6

Метод построения с помощью изоклин

Суть метода изоклин заключается в замене в дифференциальном уравнении фазовой траектории , дифференциал на константу . Тогда получается обыкновенное уравнение вида y=f(x,m).

Построение фазовой траектории начинается с построения изоклин y=f(x,m) с различными значениями m. В этом случае m будет обозначать угловой коэффициент касательной к фазовой траектории, которая пересекает данную изоклину. Пример построения с помощью изоклин приведен на рисунке 9.7.

Если нелинейный элемент имеет сложную характеристику, то предварительно необходимо с помощью кусочно-линейной аппроксимации разбить нелинейную характеристику на отдельные линейные участки. Для каждого участка необходимо вывести уравнения изоклин y=f(x,m). Построенные таким образом фазовые траектории необходимо объединить на одной плоскости согласно первоначальным диапазонам.

(необходимо рассмотреть какой-либо пример).

Вопрос