Z преобразование. Передаточная функция импульсных систем. Теорема Котельникова.

Понятие импульсной САУ.

Импульсные системы отличаются от непрерывных тем, что сигнал воздействия на объект управления в них подается импульсами в определенные промежутки времени. Импульсную систему можно разделить на две составляющие (рисунок 11.1) - непрерывную часть НЧ (линейную и нелинейную) и импульсный элемент ИЭ, который преобразует непрерывный сигнал e(t) в импульсную последовательность h(t).

Этот процесс называют квантованием. Различают квантование по уровню и по времени.

Понятие непрерывного сигнала, решетчатой функции, и импульсной функции. Их взаимосвязь.

Для исследования импульсных систем ИЭ представляется в виде дискретизатора Д и формирователя Ф (рисунок 11.2).

Дискретизатор преобразует непрерывный сигнал e(t) в последовательность отсчетов e[nT_д] – так называемую решетчатую функцию (T_д – период дискретизации, время через которое ключ Д периодически замыкается). Главное отличие решетчатой функции от непрерывной в том, что решетчатая функция существует только в моменты замыкания ключа Д (узлах решетки). В остальное время она просто не существует.

.

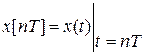Для того чтобы свести все виды импульсных сигналов к одному виду с точки зрения математического описания вводится понятие формирователя Ф, который преобразует поданную на него решетчатую функцию e[nT_д] в импульсный сигнал h(t). Так как на выходе формирователя образуется непрерывный по времени сигнал (существующий в любой момент времени), то передаточная функция Ф может быть отнесена к непрерывной части.

Чтобы на вход непрерывной части можно было подать решетчатую функцию, ее необходимо преобразовать в непрерывную. Для этого вводится понятие импульсной функции, представляющей собой множество дельта функций d(t), отстоящих друг от друга на расстояние T_д и модулированных значениями узлов решетки:

.

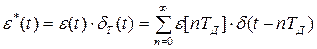Таким образом, импульсная функция непрерывна по времени, и одновременно сохраняет свойства решетчатой функции.

Z преобразование решетчатой функции. Свойства Z преобразования.

Как и в случае с непрерывными сигналами удобно отойти от временной области. Для решетчатых функций существует Z преобразование:

,

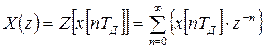где X(z) является изображением решетчатой функции x[nT_Д], z - комплексное число.

В итоге получается степенной ряд с бесконечным числом слагаемых, который может сходится (иметь конечную сумму) при определенных z. Эта область называется областью сходимости.

Примеры Z преобразования.

1) x[nT_д]={0;1;2;3;2;1;0;0;…}

.

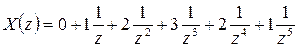Ряд имеет конечную сумму, если |z|≠0.

2) единичный ступенчатый сигнал x[nT_Д]=1;

.

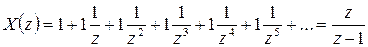Ряд сходится при |z|>1.

3) экспоненциальный сигнал x[nT_Д]=e^-n×α

.

Ряд сходится при |z|>1.

Обратное Z преобразование позволяет найти решетчатую функцию по ее изображению.

Теоремы Z-преобразования (свойства):

1) теорема линейности: Z{a₁*f₁[nT]+b₁*f₂[nT]}=a₁Z{f₁[nT]}+b₁Z{f₂[nT]};

2) теорема сдвига: ;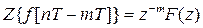

3) теорема свертки: ;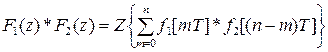

Передаточная функция импульсных систем W(z).

Рассмотрим подачу единичного ступенчатого сигнала на разомкнутую импульсную систему, состоящую из дискретизатора с периодом дискретизации T_Д и непрерывной части с передаточной функцией W(p) (например апериодическое звено).

Из рисунка 11.3 видно, что в различных точках:

y₁[0]=(x×ω)₁=x[0]×ω[0]; (индекс – номер точки по рисунку).

y₁₁[T_Д­]= (x×ω)₂+(x×ω)₅=x[0]×ω[T_Д]+x[T_Д]×ω[0];

y₁₂[2T_Д­]= (x×ω)₃+(x×ω)₆+(x×ω)₈=x[0]×ω[2T_Д]+x[T_Д]×ω[T_Д]+x[2T_Д]×ω[0];

y₁₃[3T_Д­]= (x×ω)₄+(x×ω)₇+(x×ω)₉+(x×ω)₁₀=

=x[0]×ω[3T_Д]+x[T_Д]×ω[2T_Д]+x[2T_Д]×ω[T_Д]+x[3T_Д]×ω[0];

где ω[n] – решетчатая функция импульсной характеристики непрерывной части.

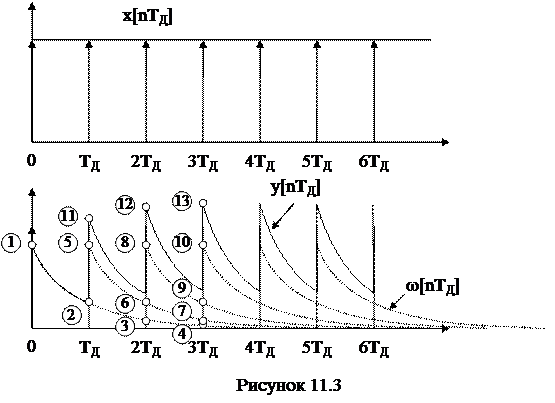
Тогда в общем виде:

y[nT_Д]= x[0]×ω[nT_Д]+x[T_Д]×ω[(n-1)T_Д]+x[2T_Д]×ω[(n-2)T_Д]+

+x[3T_Д]×ω[(n-3)T_Д]+…

По теореме свертки: Y(z)=W(z)*X(z), или

.

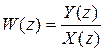W(z) называется передаточной функцией импульсной системы и есть отношение Z изображения выходного сигнала на Z изображение входного сигнала.

Зная передаточную функцию непрерывной части можно определить передаточную функцию импульсной системы путем подстановки:

(p-p_i) → (1-z^-1e^pi×Tд).

Например:

.

Дискретное преобразование Лапласа. Взаимосвязь между частотными характеристиками непрерывного и дискретного сигналов.

Под дискретным преобразованием Лапласа понимают преобразование Лапласа над импульсной функцией x^*(t):

X^*(p)=L[x^*(t)].

Очевидно, что есть взаимосвязь между изображением непрерывного сигнала X(p) и изображением импульсной функции X^*(p):

То есть частотные характеристики дискретизированного сигнала есть сумма частотных характеристик непрерывного сигнала, сдвинутых относительно друг друга на частоту дискретизации .

При этом возможны две ситуации:

1) максимально высокочастотная составляющая непрерывного сигнала меньше половины частоты дискретизации. В этом случае соседние частотные характеристики не смешиваются между собой (рисунок 11.4). Для выделения непрерывного сигнала из импульсной последовательности достаточно применить полосовой фильтр с полосой пропускания до ω_Д/2.

2) максимально высокочастотная составляющая непрерывного сигнала больше половины частоты дискретизации. В этом случае соседние частотные характеристики складываются и частотная характеристика импульсного сигнала искажается (рисунок 11.5). При этом информация об исходном сигнале безвозвратно искажается (теряется) и отфильтровать импульсную последовательность не удастся.

Теорема Котельникова:

Если функция не содержит частот, превышающих половины частоты дискретизации, то она полностью определяется своими значениями в дискретные моменты времени, отстоящие друг от друга на время T=2π/ω_Д. Функция, в этом случае, может быть полностью восстановлена из импульсной последовательности.

Вопрос