Теоретические расчеты балки. Опытная балка запроектирована и изготовлена таким образом, что ее разрушение по нормальному сечению происходит по случаю 1

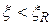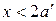Опытная балка запроектирована и изготовлена таким образом, что ее разрушение по нормальному сечению происходит по случаю 1, причем сжатая продольная арматура в работе не участвует, т.е. выполняются следующие условия: и . Контрольные нагрузки по раскрытию трещин и деформациям назначаются для стадии II (стадии работы с трещинами или стадии эксплуатации).

При расчетах необходимо установить следующие теоретические параметры балки: момент, при котором появляются трещины 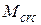; ширину раскрытия трещин 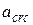и прогиб балки 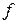при контрольной нагрузке; несущую способность балки по изгибающему моменту .

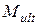Несущая способность нормального сечения изгибаемого элемента прямоугольного сечения c одиночной арматурой определяется по формуле:

, (3.10)

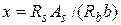. (3.11)

Момент появления трещин вычисляют по формуле:

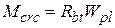. (3.12)

Здесь 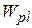упругопластический момент сопротивления:

, (3.13)

где – коэффициент приведения арматуры к бетону; 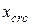– высота сжатой зоны в момент, предшествующий образованию трещин:

. (3.14)

Ширина раскрытия трещин в балке, армированной гладкой арматурой, при контрольном моменте по раскрытию трещин 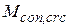определиться по формуле:

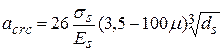, (3.15)

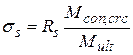, (3.16)

, (3.17)

где 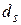– диаметр продольной растянутой арматуры, мм;

– коэффициент армирования сечения балки.

Прогиб балки в середине пролета при наличии контрольного изгибающего момента по деформациям 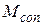, вычисляют по формуле:

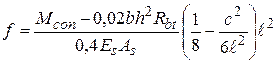, (3.18)

где 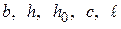– см. рис. 3.3, 3.4.

Все результаты расчетов заносятся в журнал лабораторных работ.