
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические расчеты балки
В лабораторной работе № 4 разрушение балки по наклонному сечению предусмотрено от поперечной силы по схеме 3. Несущая способность наклонного сечения по поперечной силе может быть определена из выражений:
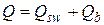 , (4.4)
, (4.4)
 , (4.5)
, (4.5)
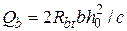 . (4.6)
. (4.6)
В выражениях (4.2) – (4.3):  и
и 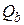 – составляющие поперечной силы, воспринимаемые соответственно хомутами и бетоном по наклонному сечению;
– составляющие поперечной силы, воспринимаемые соответственно хомутами и бетоном по наклонному сечению; 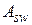 – площадь сечения хомутов;
– площадь сечения хомутов; 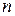 – количество хомутов, пересекаемых наклонной трещиной;
– количество хомутов, пересекаемых наклонной трещиной; 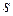 – шаг хомутов;
– шаг хомутов; 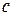 – длина горизонтальной проекции наклонной трещины на продольную ось:
– длина горизонтальной проекции наклонной трещины на продольную ось:
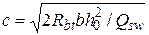 . (4.7)
. (4.7)
Значения главных растягивающих напряжений, при которых появились наклонные трещины, вычисляют по формуле:
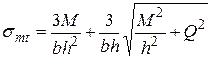 , (4.8)
, (4.8)
где 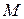 и
и 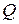 – изгибающий момент и поперечная сила в средней части наклонного сечения при появлении первой трещины.
– изгибающий момент и поперечная сила в средней части наклонного сечения при появлении первой трещины.
Ширина раскрытия наклонной трещины при контрольной поперечной силе по раскрытию трещин:
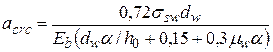 . (4.9)
. (4.9)
Напряжения в хомутах, пересекаемых наклонной трещиной:
 , (4.10)
, (4.10)
где 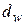 – диаметр хомутов, см;
– диаметр хомутов, см;
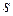 – шаг хомутов;
– шаг хомутов;
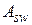 – площадь хомутов в одном сечении (в нашем случае площадь одного поперечного стержня);
– площадь хомутов в одном сечении (в нашем случае площадь одного поперечного стержня);
 – коэффициент приведения арматуры к бетону.
– коэффициент приведения арматуры к бетону.
Коэффициент армирования наклонного сечения вычисляют по формуле:
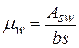 . (4.11)
. (4.11)
С учетом (4.4) – (4.7) значение разрушающей поперечной силы определяют по формуле:
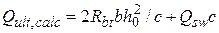 , (4.12)
, (4.12)
где 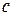 – должно удовлетворять условию
– должно удовлетворять условию 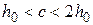 .
.
Тогда нагрузка, соответствующая теоретической разрушающей по поперечной силе, может быть вычислена по формуле:
 , (4.13)
, (4.13)
где 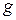 и
и  – значения нагрузок от собственного веса балки и загрузочных устройств соответственно.
– значения нагрузок от собственного веса балки и загрузочных устройств соответственно.
Прогиб балки определяют по формуле (3.18). Все расчеты и их результаты должны быть приведены в журнале испытаний.
Дата добавления: 2015-02-09; просмотров: 226; Мы поможем в написании вашей работы!; Нарушение авторских прав |