
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Социометрический метод
Социометрический метод применяется для определения отношений между людьми в каком-либо коллективе. Впервые он был использован американским психологом Дж. Морено. В нашей стране этот метод используется в области социальной психологии.
ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ ИССЛЕДОВАНИЯ
Для установления взаимосвязей между отдельными фактами и условиями в исследовании широко применяется математическая обработка.
Так, если мы пытаемся определить время с момента подачи сигнала до момента реакции испытуемого (например, время реакции на предъявляемую информацию), то окажется, что оно будет различным не только у разных людей, но и у одного человека при каждом повторном измерении. Происходит это в результате неодинаковой собранности или готовности испытуемого, влияния внешних помех, неточности (даже высокоточного) прибора, фиксирующего время, и ряда других причин. Подобное явление называют разбросом данных измерений. Особенно типично оно для измерений в психологических исследованиях. И это не случайно: каждое явление здесь связано с множеством условий и причин, сплошь и рядом не поддающихся уравниванию (хотя к этому и стремятся).
Таким образом, измерения в психологических исследованиях носят вероятностный характер. За истинную принимается некоторая средняя (центральная) величина из множества измерений ai. В качестве таковой чаще всего принимают среднее арифметическое (М), медиану (Ме) или моду (Мо).
 Среднее арифметическое (М; в некоторых источниках обозначаемая х) есть результат деления суммы всех отдельных измерений на их количество. Например, среднее арифметическое М тринадцати измерений ai: 10, 8, 9, 13, 9, 7, 10, 14, 12, 8, 10, 12, 11 — равняется 10,2:
Среднее арифметическое (М; в некоторых источниках обозначаемая х) есть результат деления суммы всех отдельных измерений на их количество. Например, среднее арифметическое М тринадцати измерений ai: 10, 8, 9, 13, 9, 7, 10, 14, 12, 8, 10, 12, 11 — равняется 10,2:
10+8+9+13+9+7+10+14+12+8+10+12+11
М = ————————————————————— = 10,2
Медиана (Ме) — это величина измерения, равноудаленная от начала и конца измерений, выстроенных по возрастающей. Например, в ряду названных выше величин ai, расположенных по возрастающей (7, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 14), медианой будет величина 10, удалённая на 7 знаков от начала и конца ряда.
Мода (Мо) — величина, наиболее часто повторяющаяся в процессе измерений; в нашем примере это тоже величина 10, повторившаяся три раза.
Достоверность каждой из этих трёх величин (М, Ме, Мо) зависит от меры симметричности распределения показателей измерений ai, которая наглядно выражается на полигоне частот измерений (см. рис.1). Исследования показывают, что распределения частот в психологических измерениях носят сплошь и рядом несимметричный характер, а поэтому наиболее достоверной величиной является мода (Мо). Однако моду можно использовать лишь при значительном количестве измерений, при малом она может не проявиться или оказаться случайной.
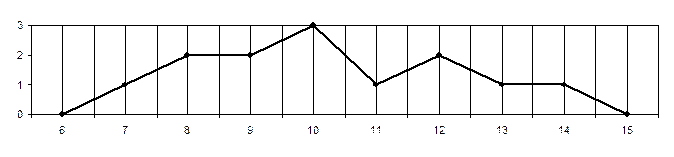
Рис. 1. Полигон частот (величины замеров условные)
Степень доверия к полученным в ходе исследования данным зависит от степени разброса величин измерений ai. В качестве величины, характеризующей разброс данных (дисперсию), в психологии чаще всего используют величину среднего квадратичного отклонения (σ). Определяется она по формуле:

 σ == ± ΣΔi 2
σ == ± ΣΔi 2
 n для большого количества измерений и
n для большого количества измерений и

σ == ± ΣΔi 2 для малого количества измерений, где
 n - 1
n - 1
где Δi — отклонение каждого отдельного измерения (ai) от средней арифметической (М);Δ ═ ai − M;
 n — количество измерений;
n — количество измерений;
Σ — знак суммы.
Эта величина показывает, что ⅔ измерений по своей величине находится в пределах М±σ. Измерения, отличающиеся от величины, принятой за истинную (М, Ме, Мо), более чем на 3σ, из расчётов принято исключать, как заведомо ошибочные.
Вычисление σ покажем на примере данных, уже известных нам по расчёту средней арифметической М:
| i | ai | Δ ═ ai − M | Δi2 |
| ― 0,2 ― 2,2 ― 1,2 1,8 ― 1,2 ― 3,2 ― 0,2 3,8 1,8 ― 2,2 ― 0,2 1,8 0,8 | 0,04 4,84 1,44 3,24 1,44 10,24 0,04 14,44 3,24 4,84 0,04 3,24 0,64 | ||
| Σ | 47,72 |
Таким образом: Σai = 133; М = 10,2; ΣΔi2 = 47,72.
Отсюда


ΣΔi2 47,72
σ ═ ± ——— = ± ———— ≈ ±2.
n – 1 12
Взаимосвязь между различными показателями, или условиями и психологическими показателями принято характеризовать коэффициентом корреляции между ними (r), который определяется по формуле (приводим одну из общепринятых):
Σ (ai − Ma) (bi − Mb)
r = ———————————
n σa σb
где a и b – величины измерений первого (a) и второго (b) ряда;
n − количество измерений;
σa , σb − среднеквадратичное отклонение измерений первого и второго ряда.
Вычисления обычно производят, используя таблицу. В качестве примера определим коэффициент корреляции между показателями успеваемости десяти студентов по психологии (a) и биохимии (b) в оценках по пятибалльной системе за год.
| i | ai | bi | ai − Mа | (ai− Mа)2 | bi − Mb | (bi − Mb)2 | (ai − Mа) (bi − Mb) |
| − 1,3 − 1,3 − 1,3 − 0,3 − 0,3 0,7 0,7 − 0,3 1,7 1,7 | 1,69 1,69 1,69 0,09 0,09 0,49 0,49 0,09 2,89 2,89 | − 1,1 − 1,1 0,9 − 0,1 − 1,1 − 1,1 0,9 − 1,1 1,9 0,9 | 1,21 0,01 0,81 0,01 1,21 1,21 0,81 1,21 3,61 0,81 | 1,43 0,13 − 1,17 0,03 0,33 − 0,77 0,63 0,33 3,23 3,23 | |||
| Σ | 12,10 | 10,90 | 7,40 |
Таким образом: Мa = 3,7; Mb =3,9;Σ (ai ─ Мa)2 = 12,10; Σ (bi ─ Мb)2 = 10,90.√
Завершим вычисления, подставив значения в соответствующие формулы:


ΣΔi 2 12,10

 σa == ± == == ± 1,16
σa == ± == == ± 1,16
n 9


ΣΔi 2 10,90



 σb == ± == == ± 1,10
σb == ± == == ± 1,10
n 9
Σ (ai − Mа) (bi − Mb) 7,40

 r == ± == == 0,58.
r == ± == == 0,58.
n σa σb 10·1,16·1,10
Корреляцию принято считать:
слабой – при коэффициенте от 0 до 0,3;
умеренной – при коэффициенте от 0,3 до 0,5;
заметной – при коэффициенте от 0,5 до 0,7;
высокой – при коэффициенте свыше 0,7.
При достижении коэффициентом корреляции величины, равной единице, она переходит в функциональную зависимость. Знак коэффициента корреляции может быть как положительным (прямая корреляция), так и отрицательным (обратная корреляция). В нашем примере корреляция умеренная, положительная.
Многие данные исследований могут быть выражены в виде графиков и гистограмм, что придаёт им наглядность, облегчает анализ и интерпретацию. Это особенно ярко выступает на примере динамических показателей. Например, при выработке навыка испытуемым (см. рис. 2) на выполнение заданного действия в каждый приём-повторение затрачивалось время (в сек) 29, 27, 30, 25, 20, 17, 24, 12, 9, 10. Средние показатели испытуемой группы из 32 человек соответственно равны: 27, 27, 26, 24, 21, 18, 16, 15, 15, 14.
 время
время
приёмы
рис. 2. Кривая выработки навыка испытуемого N и группы из 32 человек.
На этом графике четко вырисовываются особенности показателей одного испытуемого, а также закономерные изменения в падении кривой по группе в целом.
Следует иметь в виду, что мы коснулись лишь основной, простейшей количественной обработки данных исследования, которая доступна каждому.
Вданном методическом пособии кратко изложены наиболееважные ориентировки для написания традиционных научно-исследовательских студенческих работ. Дополнительную информацию вы можете найти в перечисленных ниже изданиях.
Литература
1. Ануфриев, А.Ф. Научное исследование. Курсовые, дипломные и диссертационные работы./А.Ануфриев. – М.: МГОПУ им. Шолохова, 2001. – 50 с.
2. Волков, Ю.Г. Как написать диплом, курсовую, реферат./ Ю.Г. Волков. - Ростов-на-Дону: Феникс, 2001. - 127 с.
3. Куликов Л.В. Психологическое исследование./ Л.В. Куликов - СПб.: Речь, 2001. - 183 с.
4. Кузнецов, И.Н. Научные работы: методика подготовки и оформления./И.Н. Кузнецов - Минск: Амалфея, 2000. – 544 с.
5. Непопалов, В.Н. От реферата к диплому./В.Н. Непопалов. - М.: УРАО, 2002. - 51 с.
6. Экспериментальная психология. Практикум // Под ред. С.Д.Смирнова, Т.В.Корниловой. - М.: Аспект Пресс, 2002. – 383 с.
7. Эхо Ю. Письменные работы в вузах./Ю. Эхо. - М.: Инфра-М, 2002. - 126 с.
Дата добавления: 2015-02-09; просмотров: 262; Мы поможем в написании вашей работы!; Нарушение авторских прав |