Uses crt;

Var

a,b: real; { Концы отрезка }

c: real; { Середина отрезка }

e: real; { Точность }

function f(x: real): real;

Begin

f: = sqr(x-1) - 0.5*exp(x); { Функция f(x) }

End;

Begin

writeln (' Введите концы отрезка : ');

write (' a = '); readln ( a );

write (' b = '); readln( b );

write (' Введите точность e = '); readln ( e );

writeln(' Результат : ');

while abs ( b - a ) > 2*e do

Begin

c: = ( a + b ) / 2;

if f( c ) = 0 then

Begin

writeln( ' c = ' , c : 8 : 6 , ' f( c ) = ' , f( c ) : 8 : 6 );

Readln ;

Exit ;

End;

if f(a) * f(c) < 0 then b: = c else a: = c;

End;

c: = ( a + b ) / 2;

writeln( ' c = ' , c : 8 : 6, 'f( c ) = ' , f( c ) : 8 : 6 );

Readln;

End.

Были введены следующие значения: a = 0, b = 1, e = 0.0001.Получены результаты: с = 0.213287; f ( c ) = 0.000047.

Ответ: корень уравнения 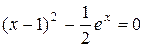равен 0,2133 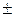0,0001.

Задания. Найти корень уравнения (если корней несколько, взять наименьший положительный) с точностью 0,0001.

Таблица 2.

№ варианта	Уравнение	№ варианта	Уравнение

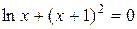
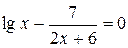
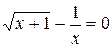
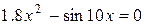
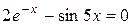
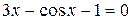
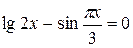
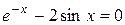
2. Решение систем линейных алгебраических уравнений

Системы линейных алгебраических уравнений (СЛАУ) широко используются во многих областях прикладной математики. Оставляя за рамками данной работы вопросы теории линейных систем, отметим, что некоторые СЛАУ могут вообще не иметь решения или иметь бесконечное множество решений. В дальнейшем мы будем рассматривать только системы, имеющие единственное решение.

В общем виде система из n уравнений с n неизвестными выглядит так:

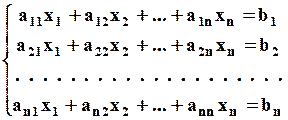
(2.1)

Таким образом, даны квадратная матрица коэффициентов при неизвестных {a_ij}, i, j = 1, 2, … , n, и вектор-столбец свободных членов (правых частей уравнений) {b_i }, i = 1, 2, … , n. В результате решения требуется определить n неизвестных x₁, x₂, … , x_n, которые удовлетворяют одновременно всем уравнениям системы.

Все методы решения СЛАУ делятся на две группы – прямые и итерационные. Прямые методы дают решение после выполнения конечного числа операций. Эти методы достаточно универсальны, но в ряде случаев полученное решение не является достаточно точным. Итерационные методы используют последовательные приближения (итерации) к искомому результату. Они позволяют получить решение с любой заданной точностью, но при их использовании заранее неизвестно количество предстоящих итераций, более того, итерационные методы в некоторых случаях вообще не дают решения.

В данном пособии мы рассмотрим по одному методу из каждой группы.