Label 1,2,3;

const n=3;

var a:array [1..n,1..n] of real;

b,x:array [1..n] of real;

i,j,k,m:integer;

e,s,d,d1,c:real;

Begin

{Ввод исходных данных}

for i:=1 to n do

Begin

writeln (‘Введите коэффициенты уравнения’,i);

for j:=1 to n do read (a[i,j]);

writeln (‘Введите свободный член уравнения’,i);

readln (b[i]);

End;

writeln ('Введите точность');readln (e);

writeln ('Введите допустимое кол-во итераций');readln (m);

for i:=2 to n do x[i]:=0;

{Решение системы}

k:=1;

Repeat

d1:=0;

for i:=1 to n do

Begin

s:=0;

for j:=1 to n do

Begin

if i=j then goto 1;

s:=s+a[i,j]*x[j];

End;

c:=(b[i]-s)/a[i,i];

d:=abs(c-x[i]);

if d1<d then d1:=d;

x[i]:=c;

End;

k:=k+1;

if k>m then goto 2;

until d1<e;

{Вывод результатов}

writeln (‘решение системы’);

for i:=1 to n do write (x[i]:8:4);

Writeln; goto 3;

2: writeln ('Количество итераций выше допустимого');

End.

Задания. Решить систему линейных алгебраических уравнений.

Таблица 3.

№ варианта	Система	Метод решения
		Метод Гаусса
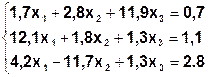
		Метод Гаусса-Зейделя ( )
		Метод Гаусса
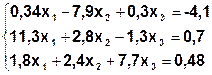
		Метод Гаусса-Зейделя ( )
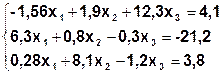
		Метод Гаусса
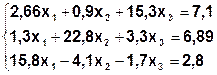
		Метод Гаусса-Зейделя ( )
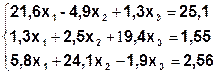
		Метод Гаусса
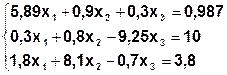
		Метод Гаусса-Зейделя ( )
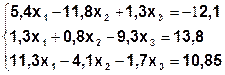
		Метод Гаусса
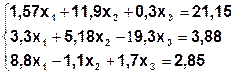
		Метод Гаусса-Зейделя ( )

3. Аппроксимация функций с помощью метода