Лабораторная работа № 9. Многомерный поиск. Методы безусловной минимизации

Задание:Найти положение точки экстремума и экстремальное значение целевой функции методом наискорейшего спуска (подъема) с точностью 0,001, если заданы координаты исходной точки .

№ варианта	Вид целевой функции f(x)	Координаты исходной точки	Экстремум
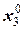
	x12 + x22- 0,5x1 - 1,6x2 + 2			-	Min
	x14 + x24 + 2x12x22 - 4x1 + 3			-	Min
	3,2 - (x1 - 1)2 - (x2 - 3)2 – 4(x3 + 5)2		-1		Max
	1 – 2x1 - 2x2 - 4x1x2 + 10x12 + 2x22			-	Min
	(x12 + x2 - 8)2 + (x1 + x22 - 18)2 + 3			-	Min
				-	Min
	(x1 - 2,4)2 + x22 – 3		-2	-	Min
	x13 + 8x23 - 6x1x2 + 1			-	Min
	4 - (x12 + x2 - 18)2 - (x1 + x22)2	-2		-	Max
				-	Max
		-1	-1	-	Min
	(x1 + 0,5)2 + 2(x2 + 3,6)2 + (x3 - 1)4 + 1		-5		Min
	x12 + x22 - 2(x1 + 2x2) + 7,35			-	Min
	X12 + x1x2 + x22 - 6x1 - 9x2			-	Min
	6 - (x12 + x2 – 11)2 - (x1 + x22 - 7)2			-	Max
	x13 + x22 – 3x1 - 2x2 + 2			-	Min
	(x1 - 2)2 + 2x22 + 5,5			-	Min
	4 - 4(x1 – 0,9)2 - 1,5(x2 + 1,6)4 - 0,8(x3 - 3,5)2	-1	-2		Max
			-3	-	Min
	x13 + x1x22 + 6x1x2 – 2	-1	-1	-	Max
				-	Max
	4x12 + x22 – 12(x1 + x2) + 46			-	Min
	(x1 - 4)2 + 5(x2 + 3)2 + 7(x3 + 0,5)2 + 10			-2	Min
	2x12 + 3(x2 - 1,5)2 + 1	-1		-	Min
	(x1 - 2,5)2 + (x2 + 4)2 + 8		-1	-	Min
				-	Min
	4 – 2(x1 – 3)2 - (x2 - 2)2 – 3(x3 + 1)4		-3		Max
	(x12 + x2)2 + (x1 + x22 - 18)2 + 4		-2	-	Min
	(x12 + x2 - 7)2 + (x1 + x22 - 11)2 + 3			-	Min
	x12x2 + x23 + 6x1x2 + 1		-1	-	Max
	2(x1+2)2 + (x2-1.5)2 +3(x3-1)2	-1			Min
	x12 + x1x2 + x22 –3x1 - 6x2	-2		-	Min
	(x1-1)2 + (x2-3)2 + 4	-3		-	Min
	2x13 – x1x22 + 5x12 +3x22 + 2	-1		-	Min
	x12 + x22 – 2x1 - 3x2 + 2			-	Min
	6x1x2 - 8x13 - x23 – 3			-	Max
	x13 + x22 – 15x1x2			-	Min
	2(x1 + x2 – x12) + 4x1x2 – 10x22 – 5	-1		-	Max
				-	Min
					Max
				-	Max
				-	Max
			-1	-	Min
			-1	-	Min
				-	Min
		-1		-	Min
		-2		-	Max
				-	Max
		-1	-3		Min
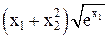
			-2	-	Min

Вопросы для самоподготовки

1. В чем состоит общая задача нелинейного программирования?

2. На какие группы делятся методы решения задач безусловной минимизации?

3. Дайте краткую характеристику методов безусловной минимизации: итерационный характер методов; проблема выбора шага; выбор направления поиска.

4. Опишите алгоритм метода покоординатного спуска.

5. Как выбирается направление спуска в методе покоординатного спуска?

6. При выполнении какого условия следует прекратить поиск?

7. Составьте блок-схему метода покоординатного спуска.

8. Дайте сравнительную характеристику градиентных методов оптимизации.

9. Дайте описание алгоритма метода наискорейшего спуска.

10. Как решается проблема выбора шага и направления в методе наискорейшего спуска?

11. Дайте описание алгоритма метода сопряженных направлений.

12. В чем состоит основное отличие методов наискорейшего спуска и сопряженных направлений?

13. Какие методы условной минимизации вы знаете?

14. В чем главное отличие методов условной минимизации от методов безусловной минимизации?

15. Метод сканирования.

16. Каково минимальное количество вычислений целевой функции для метода сканирования?

17. Укажите область использования метода сканирования.

18. Метод штрафных функций.

19. На какие классы можно разделить методы штрафных функций?

20. Чем характеризуются параметрические методы?