Бюджетная линия. Бюджетная линия показывает различные комбинации двух товаров, которые могут быть приобретены при фиксированной величине денежного дохода.

Бюджетная линия показывает различные комбинации двух товаров, которые могут быть приобретены при фиксированной величине денежного дохода.

Предположим, что в распоряжении потребителя имеются 600 ден.ед., которые он готов потратить на покупку товара А и товара В. Допустим, что цена товара А составляет 60 ден. ед. за 1 кг, а товара В – 40 ден. ед. Потребитель может купить различные комбинации товара А и товара В на имеющиеся 600 ден. ед., например 10 кг товара А и 0 кг товара В или 15 кг товара В и 0 кг товара А, или 4 кг товара А и 9 кг товара В и т.д. На основании данных комбинаций построим бюджетную линию потребителя (рис. 8.5).

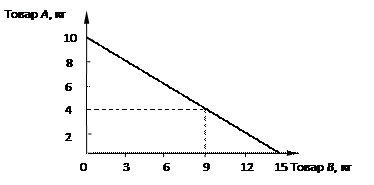Рис. 8.5. График бюджетной линии

Любая точка, лежащая на прямой, удовлетворяет уравнению:

P_АQ_А + P_ВQ_В = Y, где

P_А, P_В – цены товара А и товара B;

Q_А, Q_В – количество товара A и товара B;

Y – доход потребителя.

Совместив кривые безразличия и бюджетную линию, можно
ответить на вопрос: какую комбинацию товаров выберет потребитель (рис. 8.6).

Рис. 8.6. График максимизации потребностей потребителя

Потребитель не выбирает точки M и N, ибо они лежат на кривой безразличия С, находящейся ниже кривой D, а потому приносят меньше удовлетворения. С кривой безразличия Е бюджетная линия не имеет общих точек. Следовательно, в своем выборе потребитель остановится на точке, где бюджетная линия является касательной к кривой безразличия D. В точки K достигается максимум полезности для потребителя. Другие иные точки либо уступают ей по уровню полезности, либо недостижимы при имеющемся бюджете. Именно в этой точке достигается максимально возможное удовлетворение потребителя при полном использовании его дохода.

8.6 Кривые «доход-потребление» и «цена-потребление»

Точка максимума полезности для потребителя отражает статическую ситуацию, когда ни его доход, ни цены товаров не меняются. В действительности такие изменения происходят постоянно, вызывая перемещения бюджетной линии.

Смещение бюджетной линии вправо-вверх происходит в двух случаях:

1. при росте дохода и неизменных ценах;

2. при неизменном доходе и снижающихся ценах.

При этом каждое смещение бюджетной линии вправо-вверх приводит ее к касанию с новой кривой безразличия повышенного уровня потребления.

Все точки, отражающие последовательный рост потребления под влиянием возрастающего дохода и соединенные в единую линию, называются кривой «доход-потребление» или кривой уровня жизни Е (рис. 8.7).

Рис. 8.7. Кривая «доход-потребление»

На графике видно, что с ростом дохода потребление товаров увеличивается, т.е. кривая «доход–потребление» является восходящей.

Изменения снижения цен при неизменном доходе показывает кривая «цена-потребление». Если понизится цена лишь одного товара, то смещение бюджетной линии произойдет только вдоль той оси, где этот товар представлен. На рис. 8.8 показаны снижения цен на товар В и, соответственно, смещения бюджетной линии по оси В, вправо.

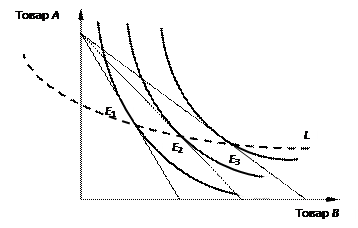Рис. 8.8. Кривая «цена–потребление»

Известно, что максимум потребностей для потребителя достигается в точке касания бюджетной линии к кривой безразличия. Если через все точки касания провести соединительную линию, то получим кривую «цена-потребление» L.

Кривая «цена–потребление», во-первых, служит объяснением кривой индивидуального спроса. По мере снижения цен и смещения бюджетной линии вправо потребление товара В растет. Другими словами, из кривой L вытекает обратная зависимость между ценой и количеством закупок по этой цене (закон спроса). Во-вторых, кривая «цена-потребление» показывает влияние изменения цен на замещение одного товара другим.