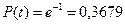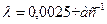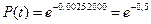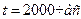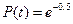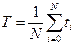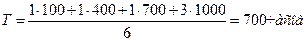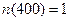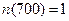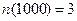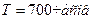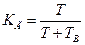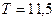КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зачет Д-410-3 Билет № 16
| № п/п | Содержание вопроса | ||||||||||||
| В чем отличие понятий «Не исправное состояние» и «Не работоспособное состояние»? Объект может быть признан неработоспособным лишь в том случае, если хотя бы один из его параметров по результатам контроля не соответствует нормам. Поскольку исправность более широкое понятие, чем работоспособность, то вполне логичной является ситуация, при которой неисправный объект, например, по требованиям внешнего вида, может быть работоспособным с точки зрения выполнения функций, но не наоборот. | |||||||||||||
Каким образом связаны между собой вероятность отказа и частота отказа? Какое из свойств надежности характеризуют указанные показатели?.
Вероятность отказа Q(t) - это вероятность того, что наработка изделия до отказа T будет меньше заданного времени t.
Вероятность отказа Q(t) является функцией распределения случайной величины T и изменяется от 1 до 0. Характер зависимости вероятности отказа от времени показан на рис. 1.
Вероятность безотказной работы- это вероятность того, что в пределах заданной наработки отказ объекта не возникнет (ГОСТ 27.002-89), т.е.:
P(t) = P(T >t).
Рис. 1. В теории надежности плотность распределения f(x) случайной величины T называют частотой отказов а(t). Частота отказа а(t) - характеризует скорость изменения функции надежности Q(t) в данный момент времениt (характеризует распределение времени работы до отказа).
Итак, по определению
Статистическое значение частоты отказов а(t)* можно получить следующим образом:
где n(t) = n(t1 + Dt) n(t1) - число отказов за время t.
Физическое толкование выражения: частота отказов показывает, какая доля от первоначального числа включенных в работу изделий отказывает в единицу времени в любой период работы. Эти показатели характеризуют такое свойство надежности, какбезотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки. Свойство безотказности проявляется как при использовании объекта по назначению, так и в периоды хранения и транспортирования. | |||||||||||||
При ориентировочном расчете надежности принимается допущение о том, что все элементы проектируемого устройства функционируют на этапе нормальной эксплуатации. Каким образом это допущение используется в методике расчета.
На участке нормальной эксплуатации значение интенсивности отказов практически постоянно, то есть не зависит от времени, следовательно, можно записать: l(t) =const.
Выражение для определения вероятности безотказной работы имеет вид:
 (*),
Таким образом, при l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение (* ) называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ (*),
Таким образом, при l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение (* ) называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ 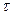 не зависит от предшествующей наработки, а определяется только длиной интервала не зависит от предшествующей наработки, а определяется только длиной интервала 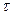 : :
 Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
 Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять
Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять  ; ; 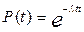 , то справедливо выражение , то справедливо выражение
 Тогда вероятность безотказной работы будет равна:
Тогда вероятность безотказной работы будет равна:
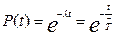 Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
| |||||||||||||
Поясните сущность доверительного интервала при экспериментальной оценке показателей надежности.
Доверительная вероятность определяет достоверность оценки параметра, а доверительный интервал - ее точность.
Определение опытным путем неизвестного параметра надежности с указанием, в каком интервале и с какой вероятностью находится его значение, называется интервальной оценкой. Заключение о соответствии показателей надежности заданным требованиям делается только на основе интервальной оценки.
Рассмотрим способ интервальной оценки средней наработки до отказа невосстанавливаемой аппаратуры. Этот способ распространяется также и на оценку наработки на отказ восстанавливаемой аппаратуры при простейшем потоке отказов, для которого время работы между отказами распределено по экспоненциальному закону.
Интервальная оценка может быть установлена лишь в том случае, если кроме числа наблюдений n и зафиксированных значений исследуемой случайной величины известен еще и закон распределения последней. Отличие законов распределения обусловливает отличие способов получения интервальной оценки. В последующих рассуждениях будем считать, что для времени работы до отказа имеет место экспоненциальный закон распределения.
Задача заключается в том, чтобы при известном законе распределения случайной величины T экспериментально определить неизвестное значение параметра закона и установить, насколько опытная величина отличается от истинного значения.
Для решения задачи необходимо предварительно распределить вероятности нахождения истинного значения средней наработки до отказа T вне доверительного интервала - левее и правее его. Целесообразно принять обе вероятности равными с тем, чтобы риски неверного заключения о соответствии или несоответствии уровня надежности заданным требованиям были одинаковыми. Распределение вероятностей для этого случая показано на рис. 1.
Нахождение значения T в одной из трех областей: в доверительном интервале, правее или левее его - составляет полную группу событий. Из рис. 1 очевидно, что γ + 2 γ 2 = 1. Отсюда получим необходимое для расчета значение:
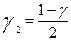 (16)
Так как согласно выражению (8) γ1 = γ + γ 2, то для расчета получим: (16)
Так как согласно выражению (8) γ1 = γ + γ 2, то для расчета получим:

| |||||||||||||
Нарисовать пример структурной схемы надежности объекта с общим резервированием элементов.

| |||||||||||||
Определить максимально возможное число элементов проектируемого объекта, если интенсивность отказов элементов не больше, чем 10-7 1/час, а средняя наработка на отказ объекта не должна быть меньше 1000 часов.
Ответ:
Ответ:
| |||||||||||||
На участке нормальной эксплуатации интенсивность отказов невосстанавливаемого объекта равна 0,001 1/ч. Какова вероятность его отказа в течение 1000 часов?
Ответ: | |||||||||||||
На испытания длительностью 1000 часов поставлено 6 невосстанавливаемых объектов. Первый объект отказал через 100 ч., второй – через 400 ч., третий – через 700 ч., а остальные не отказывали. Определить статистическое значение средней наработки до отказа.
Ответ: | |||||||||||||
| Система состоит из 2 равных по надежности восстанавливаемых элементов, причем отказ любого из них приводит к отказу системы. Определить значения наработки на отказ элементов, если известно, что для всей системы Кг = 0,92 и ТВ = 1 час
| |||||||||||||
| Пусть имеется многоканальная аппаратура передачи данных, имеющая 10 каналов связи? Пусть, также для обеспечения связи требуется только 8 каналов. Вычислите Кг аппаратуры с учетом резервирования. Назовите вид резервирования. | |||||||||||||
| Опишите модель объекта диагностирования в виде таблицы функции неисправностей. | |||||||||||||
| Приведите пример ситуации, когда условный алгоритм диагностирования оказывается менее эффективным, чем безусловный. | |||||||||||||
| Почему при построении модели объекта диагностирования в виде графа информационно-энергетических связей сначала строится как минимум два самостоятельных ГИЭС? | |||||||||||||

| Для вершин изображенного на рисунке ГИЭС определить индексы предшествования. На основе ГИЭС построить ДЛВ по структурному критерию | ||||||||||||
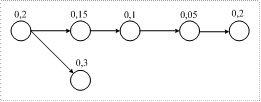
| Для вершин изображенного на рисунке ГИЭС определить значения функции предпочтительного выбора. На основе ГИЭС построить ДЛВ по вероятностному критерию |
Дата добавления: 2015-02-10; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |

 ????
????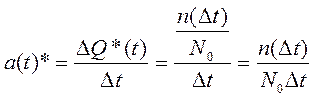
 час-1
час-1
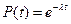
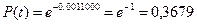
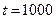 час
час