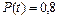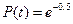КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зачет Д-410-3 Билет № 14
| № п/п | Содержание вопроса | ||||||||
В чем отличие понятий «Время работы» и «Наработка»?
Вероятность безотказной работы - это вероятность того, что в пределах заданной наработки отказ объекта не возникнет (ГОСТ 27.002-89).
Математически вероятность безотказной работы P(t) - это вероятность принятия случайной величиной Т значения не меньше некоторого наперед заданного текущего времени функционирования изделия:
P(t) = P(T >t).
 Р(t), Q(t)
 Q(t)
Р(t)
0 t Рис. 1. Кривая P(t), приведенная на рис.1, называют функцией надежности. Для данного изделия появление отказа и его отсутствие представляют полную группу несовместимых событий и поэтому: P(t) + Q(t) = 1. Q(0) = 0 P(0) = 1 Q( ¥) = 1 P( ¥) = 0 Q(t2) > Q(t1) P(t2) < P(t1) Для экспериментального определения зависимостей P(t) и Q(t) необходимо получить статистические данные об отказах при работе в одинаковых условиях большого числа изделий данного типа. Изделий ставят на испытания или под-контрольную эксплуатацию. Если из общего числа N, поставленных на испытания изделий за время t отказало n (t). Осталось исправными Nи(t) = N -n(t), то статистические значения Q*(t) и P*(t) определяются из соотношений: n(t) Nи(t) N – n (t) n(t) Q*(t)=──── ; P*(t) = ──── = ────── = 1 - ─── = 1 - Q*(t), No N N N где n(t) = N - Nи(t) - количество отказавших изделий за время t представлено кривой на рис. 2.
Средняя наработка до отказа | |||||||||
Какие свойства надежности характеризуют указанные показатели: гамма-процентный срок сохраняемости, коэффициент готовности?
гамма-процентный срок сохраняемости-это показательсохраняемости
Сохраняемость— это свойство объекта сохранять в заданных пределах значения параметров, характеризующих способности объекта выполнять требуемые функции в течение и после хранения и транспортирования. Сохраняемость изделий оценивается средним сроком сохраняемости и гамма-процентным сроком сохраняемости.
Коэффициент готовности-это комплексный показатель надежности
Коэффициент готовности - это вероятность того, что объект окажется работоспособным в произвольный момент времени, кроме планируемых периодов, в течение которых использование его по назначению не предусматривается.
Количественно коэффициент готовности равен:
Kг= 
Используется также показатель "коэффициент простоя", характеризующий вероятность застать объект находящимся на восстановлении после отказа:
Kп = 1 ‑ Kг
| |||||||||
При ориентировочном расчете надежности принимается допущение о том, что все элементы проектируемого устройства функционируют на этапе нормальной эксплуатации. Каким образом это допущение используется в методике расчета.
На участке нормальной эксплуатации значение интенсивности отказов практически постоянно, то есть не зависит от времени, следовательно, можно записать: l(t) =const.
Выражение для определения вероятности безотказной работы имеет вид:
 (*),
Таким образом, при l(t) =const распределение времени безотказной работы T подчиняется экспоненциальному закону. Выражение (* ) называют экспоненциальным законом надежности. При его использовании все задачи надежности решаются довольно просто. Отметим важное свойство этого закона: при экспоненциальном законе вероятность безотказной работы в интервале времени t+ 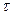 не зависит от предшествующей наработки, а определяется только длиной интервала :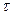
Средняя наработка до отказа при экспоненциальном законе надежности, как было определено выше, является интегральной величиной
Из этого выражения следует, что Т численно равна площади, ограниченной кривой Р(t) и осями координат. Но одна и та же площадь может быть ограничена кривыми различного вида.
Отсюда следует, что Т не полностью характеризует закон распределения отказов, а является лишь параметром. Для частного случая, когда изучается надежность изделия в период нормальной эксплуатации и можно принять  ;  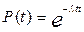, то справедливо выражение
Тогда вероятность безотказной работы будет равна:
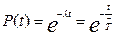Таким образом, определены основные параметры безотказности невосстанавливаемых объектов.
| |||||||||
Поясните физический смысл процессов, происходящих в период старения.
Графики имеют три характерные участка: участок приработки, на которых наблюдается повышенные значения интенсивности и частоты отказов, обусловленные скрытыми дефектами производственного характера; участок нормальной эксплуатации ; участок старения, когда снова наблюдается повышенный выход элементов из строя по причине проявления признаков старения.
На участке нормальной эксплуатации значение интенсивности отказов практически постоянно, то есть не зависит от времени, следовательно, можно записать: l(t) =const.
I период – приработки; II период – нормальной эксплуатации (внезапные отказы); III период – старения и износа (постепенные отказы) Интенсивность отказов вI период – приработки или период выжидания. В этот период средства или образцы были нагружены и оно отказывают; II период – период нормальной эксплуатации. Характерно для данного интервала, что интенсивность отказа постоянная, т.е. cons't; III период – старения в следствии физических , химических процессов, происходит ухудшение процессов старения. Поэтому интенсивность отказов увеличиваются, затем уменьшаются, т.к. количество средств связи стремится к нулю. | |||||||||
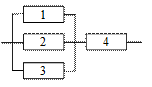
Нарисовать пример структурной схемы надежности объекта с раздельным резервированием элементов.
| |||||||||
| |||||||||
|
- это математическое ожидание (МО) случайной величины T и показывает, какова средняя продолжительность работы изделия до отказа.
Главная страница Случайная страница Контакты