Криптосистема шифрования данных RSA

Алгоритм RSA предложили в 1978г. три автора Р. Райвест (Rivest), A. Шамир (Shamir) и А. Адлеман (Adieman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как к режиме шифрования данных, так и в режиме электронной цифровой подписи [2].

Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.

В криптосистеме RSA открытый ключ , секретный ключ , сообщение М и криптограмма С принадлежат множеству целых чисел

={0,1,2,.....,N-1},

(5.5)

где N - модуль:

Здесь Р и Q-случайные большие простые числа. Для обеспечения максимальной безопасности выбирают Р и Q равной длины и хранят в секрете.

Множество с операциями сложения и умножения по модулю N образует арифметику по модулю N.

Открытый ключ Кв выбирают случайным образом так, чтобы, выполнялись условия:

, НОД

(5.7)

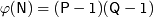
(5.8)

где - функция Эйлера

Функция Эйлера указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N. Второе из указанных выше условий означает, что открытый ключ и функция Эйлера должны быть взаимно простыми.

Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ , такой, что

(5.9)

или

Это можно осуществить, так как получатель В знает пару простых чисел (P.Q) и может легко найти , и N должны быть взаимно простыми.

Открытый ключ используют для шифрования данных, а секретный ключ - для расшифрования.

Преобразование шифрования определяет криптограмму С через пару (открытый ключ , сообщение М) в соответствии со следующей формулой:

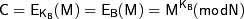
(5.10)

В качестве алгоритма быстрого вычисления значения С используют ряд последовательных возведений в квадрат целого М и умножений на М с приведением по модулю N.

Обращение функции , т.е. определение значения М по известным значениям С, И N, практически не осуществимо при .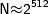

Однако обратную задачу, т.е. задачу расшифрования криптограммы С, можно решить, используя пару (секретный ключ , криптограмма С) по следующей формуле:

(5.11)

Процесс расшифрования можно записать так:

(5.12)

Подставляя в (5.12) значения (5.10) и (5.1 I), получаем:

(5.13)

Величина играет важную роль в теореме Эйлера, которая утверждает, что

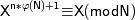
(5.14)

Сопоставляя выражения (5.13) и (5.14), получаем или, что то же самое,

Именно поэтому для вычисления секретного ключа используют соотношение (5.9).

Таким образом, если криптограмму возвести в степень то в результате восстанавливается исходный открытый текст М, так как

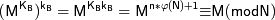
(5.14)

Таким образом, получатель D, который создает криптосистему, защищает два параметра: 1) секретный ключ и 2) пару чисел (P,Q), произведение которых, дает значение модуля N. С другой стороны, получатель В открывает значение модуля N и открытый ключ .

Противнику известны лишь значения и N. Если бы он смог разложить число К на множители Р и Q, то он узнал бы "потайной ход" - тройку чисел {Р, Q, }, вычислил значение функции Эйлера =(P-1)(Q-1) и определил значение секретного ключа . Однако, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных Р и Q составляют не менее 100 десятичных знаков).

Процедуры шифрования и расшифрования в криптосистеме RSA

Предположим, что пользователь А хочет передать пользователю В сообщение в зашифрованном виде, используя криптосистему RSA. В таком случае пользователь А выступает в роли отправителя сообщения, а пользователь В - в роли получателя. Криптосистему RSA должен сформировать получатель сообщения, т.е. пользователь В. Последовательность действий пользователей В и А.

• Пользователь В выбирает два произвольных больших простых числа Р и Q.
• Пользователь В вычисляет значение модуля N=Р*Q.
• Пользователь В вычисляет функцию Эйлера =(P-l)(Q-l) и выбирает случайным образом значение открытого ключа К, с учетом выполнения условий: , НОД
• Пользователь В вычисляет значение секретного ключа , используя

расширенный алгоритм Евклида при решении сравнения .

• Пользователь В пересылает пользователю А пару чисел (N, ) по

незащищенному каналу. Если пользователь А хочет передать пользователю В сообщение М, он выполняет следующие шаги.

• Пользователь А разбивает исходный открытый текст М на блоки, каждый из которых может быть представлен в виде числа 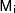= 0,1,2, ...,N-1.
• Пользователь А шифрует текст, представленный в виде

последовательности чисел 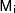, по формуле и отправляет криптограмму C1 C2, C3,..., Ci,.., пользователю В.

• Пользователь В расшифровывает принятую криптограмму C1, С2, Сз,...,Ci,...., используя секретный ключ Кв, по формуле .

В результате будет получена последовательность чисел 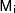, которые представляют собой исходное сообщение М. Чтобы алгоритм RSA имел практическую ценность, необходимо иметь возможность без существенных затрат генерировать большие простые числа, уметь оперативно вычислять значения ключей и .

Безопасность и быстродействие криптосистемы RSA.

Безопасность алгоритма RSA базируется на трудности решения задачи факторизации больших чисел, являющихся произведениями двух больших простых чисел.

Один из наиболее быстрых алгоритмов, известных в настоящее время, алгоритм NFS (Number Field Sieve) может выполнить факторизацию большого числа N (с числом десятичных разрядов больше 120) за число шагов, оцениваемых величиной 1/3 2/3 e2(ln n) (In (In n)).

Разработчикам криптоалгоритмов с открытым ключом на базе RSA приходится избегать применения чисел длиной менее 200 десятичных разрядов. Самые последние публикации предлагают применять для этого числа длиной не менее 250-300 десятичных разрядов.

Сделана попытка расчета оценок безопасных длин ключей асимметричных криптосистем на ближайшие 20 лет исходя из прогноза развития компьютеров и их вычислительной мощности, а также возможного совершенствования алгоритмов факторизации. Эти оценки (табл. 5.1) даны для трех групп пользователей (индивидуальных пользователей, корпораций и государственных организаций), в соответствии с различием требований к их информационной безопасности.

Таблица 5.1.Оценки длин ключей для асимметричных криптосистем, бит

Криптосистемы RSA реализуются как аппаратным, так и программным путем. Для аппаратной реализации операций зашифрования и расшифрования RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах (СБИС), позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время. И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.

Программная реализация RSA примерно в 100 раз медленнее программной реализации DBS. Малое быстродействие криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.