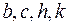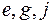КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценки хроматического числа
1.
Теорема Кенига
Граф бихроматичен (  ) тогда и только тогда, когда в
) тогда и только тогда, когда в 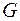 нет циклов нечетной длины.
нет циклов нечетной длины.
2.
Теорема
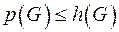 , где
, где  - плотность графа
- плотность графа 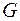 .
.
3.
Теорема
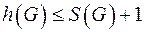 , где
, где  - степень графа
- степень графа 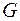 .
.
4.
Оценка Бержа
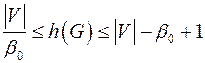 , где
, где 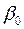 - число внешней устойчивости графа
- число внешней устойчивости графа 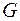 .
.
5.
Теорема
 , где
, где 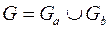 ,
, 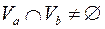 .
.
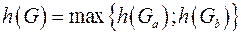 , где
, где 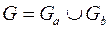 ,
,  .
.
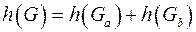 , где
, где  ,
,  .
.
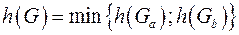 , где
, где 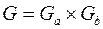 .
.
Примеры
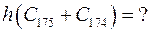
а) Графы не имеют общих вершин.
По теореме выше 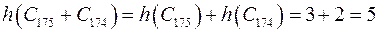 .
.
б) Графы имеют по одной общей вершине.
Отметим для нечетного цикла следующую раскраску: одна вершина в 3-й цвет, остальные в 1-й и 2-й цвета поочередно. На нашем графе вначале раскрасим в два цвета четный цикл (вместе с общей вершиной). Теперь рассмотрим нечетный цикл. В нем общая вершина оказалась закрашена каким-то цветом. Считаем этот цвет 3-им и закрашиваем все остальные вершины поочередно в два цвета (отличные от ранее выбранных, так как имеем граф суммы). Итого использовали четыре цвета. 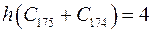 .
.
в) Графы имеют по две общие, не смежные между собой вершины.
Так как между двумя смежными вершинами в обоих графах будет располагаться цепь длиной, по крайней мере, 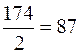 , соединенная с аналогичной цепью в другой части графа всеми возможными связями, то
, соединенная с аналогичной цепью в другой части графа всеми возможными связями, то 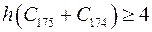 . Для четырех цветов раскраска существует всегда: сначала раскрашиваем четный цикл в два цвета, затем оставшиеся цепи нечетного цикла закрашиваем в другие два цвета.
. Для четырех цветов раскраска существует всегда: сначала раскрашиваем четный цикл в два цвета, затем оставшиеся цепи нечетного цикла закрашиваем в другие два цвета. 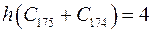 .
.
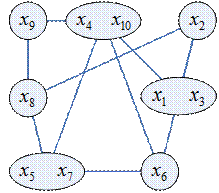
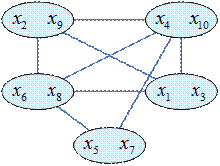
Алгоритм приближенной раскраски графа (алгоритм Ершова)
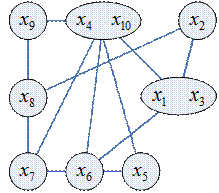
Алгоритм основан на стягивании несмежных вершин:
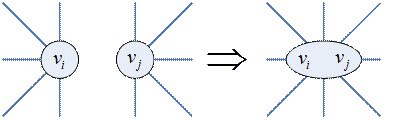
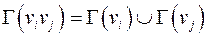
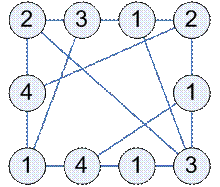
Стягивание проводить до тех пор, пока не получим полный граф. Мощность этого полного графа является оценкой хроматического числа сверху, а сам полный граф определяет приближенную раскраску графа.
Замечание
В первую очередь желательно стягивать те вершины, расстояние между которыми четно.
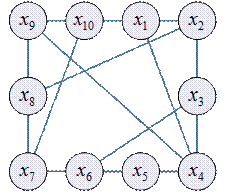
Пример
| 
| 
| 
| |
| 
| 
| 
| |

| 
| 
| 
| |
| 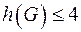
| 
| ||
Задача
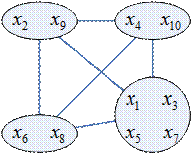
Есть 3 предприятия, на которых должны выпускаться 11 изделий. Каждый тип изделий должен выпускаться только на одном предприятии. При выпуске изделий разного типа (  ) могут использоваться общие детали и материалы. Для каждой пары изделий указан процент общих деталей и материалов. Необходимо распределить изделия по предприятиям так, чтобы на одном предприятии выпускались детали с наибольшим процентом общих деталей. Критерий: Минимум общих поставок для изделий, выпускаемых на одном предприятии был как можно больше.
) могут использоваться общие детали и материалы. Для каждой пары изделий указан процент общих деталей и материалов. Необходимо распределить изделия по предприятиям так, чтобы на одном предприятии выпускались детали с наибольшим процентом общих деталей. Критерий: Минимум общих поставок для изделий, выпускаемых на одном предприятии был как можно больше.
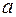
| ||||||||||

| 
| |||||||||
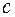
| 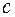
| |||||||||
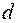
| 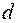
| |||||||||

| 
| |||||||||

| 
| |||||||||
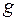
| 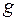
| |||||||||
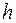
| 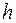
| |||||||||
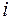
| 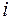
| |||||||||
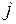
| 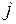
| |||||||||
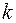
|
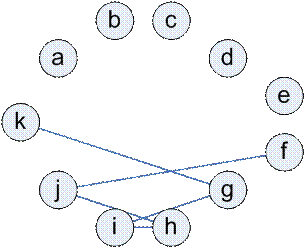
Граф несовместимости изделий 
 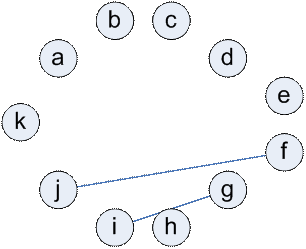 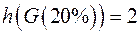
| 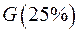  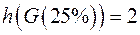
|
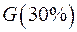  
|   
|
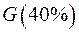 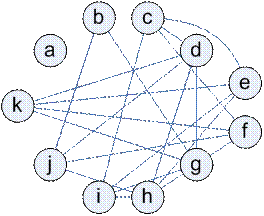
|  Раскраска: Раскраска:  
|
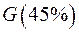 
| 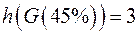 Раскраска: Раскраска: 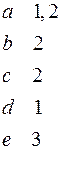 
|
 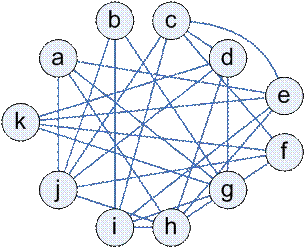
|  Раскраска: Раскраска: 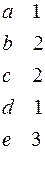 
|
 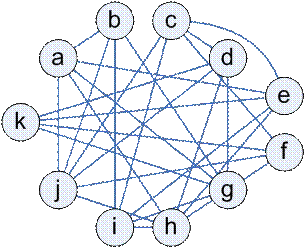
| 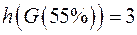 Раскраска: Раскраска: 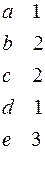 
|
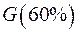 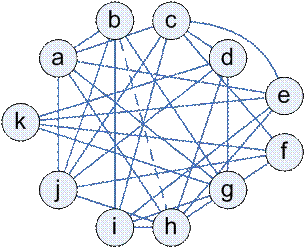
| 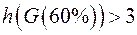 Решение - Решение - 
|
Дата добавления: 2015-02-10; просмотров: 326; Мы поможем в написании вашей работы!; Нарушение авторских прав |