Реберные графы. Графы со свойством реберности

Пусть 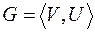- некоторый граф. Назовем граф 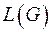реберным графом 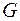, если носитель графа 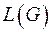совпадает с множеством ребер графа 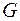, и две вершины в 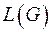смежны, если соответствующие ребра смежны в .

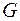Пример

(это преобразование можно выполнить всегда)

Граф 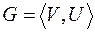обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для .

Пример

Теорема
Граф обладает свойством реберности, если существует разложение ребер графа на полные подграфы такое, что каждая вершина графа принадлежит не более чем двум полным подграфам.

Замечание
1. Не для любого графа существует такое разложение ребер.
2. В разложении ребер каждое ребро принадлежит ровно одному подграфу.

Пример

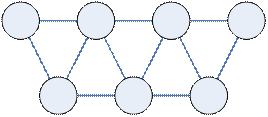
Пример

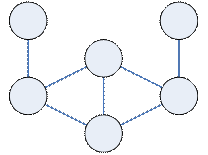
не являются реберными

Если граф обладает свойством реберности, то как найти его образ (т.е. граф, для которого данный является реберным)?

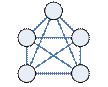
Пример

:

:

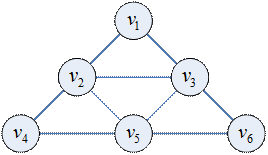
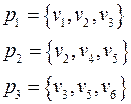
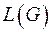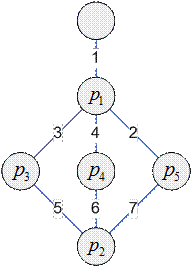
Пример

Укладки графа. Планарность

Исследуются топологические свойства графа. Гомеоморфизм графов – еще одно отношение эквивалентности на графах. Два графа 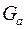и 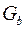гомеоморфны, если они изоморфны с точностью до цепей степени 2.

Пример

:	:
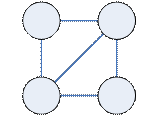
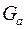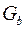Гомеоморфны. Говорят, что они имеют одну и ту же топологию.

Пусть 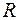- некоторая поверхность. Род поверхности 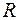- это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.

Род плоскости: 0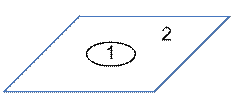
Род сферы: 0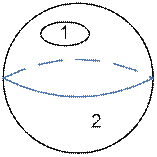
Род тора: 1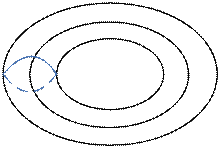

Поверхности, которые имеют род 4:

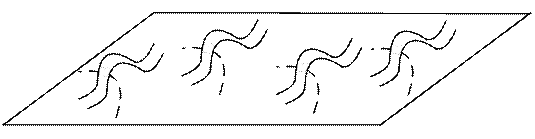
Род графа 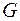- - 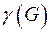минимальный род поверхности, на которой можно «уложить» граф 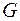без взаимных пересечений ребер (ребра пересекаются только в вершинах).

Пример

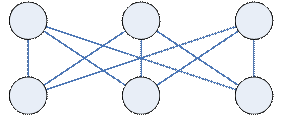
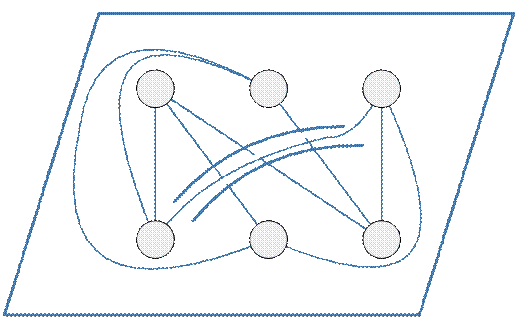
Граф 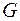называется планарным(плоским), если .

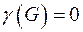· печатные платы – планарные графы;

· микросхемы (на уровне технологии их изготовления) – планарные графы.

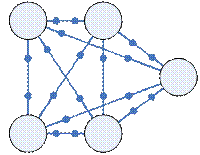
Критерий планарности графа (критерий Понтрягина-Куратовского)

Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные или .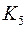

Алгоритм приведения графа 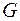к планарному

1) Найти все подграф, гомеоморфные и .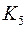
2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют.
3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).