
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перечисление графов
Группа. Группа подстановки
Группа – алгебра с одно бинарной операцией (  ), которая обладает следующими свойствами:
), которая обладает следующими свойствами:
1) замкнутость
 и
и 

2) ассоциативность

3) наличие нейтрального элемента

4) существование обратного элемента
для 
Группа подстановки. Пусть  . Подстановкой назовем
. Подстановкой назовем  .
.






| 
|


| 
|

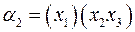
| 
|


| 
|
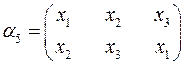

| 
|

Операция: произведение подстановок 



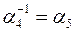
Пример

Пример

Группа автоморфизмов графа
Пусть 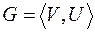 - некоторый граф. Автоморфизм графа
- некоторый граф. Автоморфизм графа  - это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
- это изоморфизм на себя (с, сохраняющая отношение смежности между вершинами графа).
Пример


 - не является автоморфизмом.
- не является автоморфизмом.
 - автоморфизм.
- автоморфизм.
Группа автоморфизмов графа  -
-  , где
, где  - множество всех автоморфизмов графа,
- множество всех автоморфизмов графа,  - операция произведения.
- операция произведения.
Пример


 :
:

Пример
 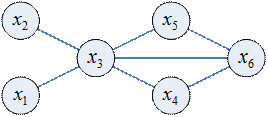
| 
|
Пример     
|         
|
Задание
Задан автоморфизм. Определить все графы, которые допускают данный автоморфизм. 

| 
|
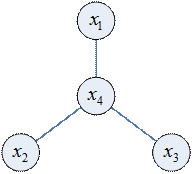
| 
|
Дата добавления: 2015-02-10; просмотров: 281; Мы поможем в написании вашей работы!; Нарушение авторских прав |