
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРОВЕРКА НОРМАЛЬНОСТИ ЗАКОНА РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ
При обработке экспериментальных данных существенное значение имеет вопрос о том, подчиняется или нет результат
измерения нормальному закону распределения вероятности. Непротиворечивость такой гипотезы должна быть обязательно проверена.
Поскольку ошибки искажают эмпирический закон распределения вероятности результата измерения, постольку проверка предположения о его нормальности производится после исключения ошибок.
Правдоподобна или нет гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, можно определить уже по виду гистограммы, построенной на основании экспериментальных данных. Порядок ее построения рассмотрен в примере 4. Наглядность отображения гистограммой закона распределения вероятности результата измерения зависит от соблюдения следующих правил при ее построении:
1) интервалы  , на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
, на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
2) число интервалов k устанавливать в соответствии со следующими рекомендациями:

3) масштаб выбирать таким, чтобы высота гистограммы относилась к основанию примерно, как 5 к 8.
Иногда по виду гистограммы можно с большой уверенностью заключить, что результат измерения подчиняется (или не подчиняется) нормальному закону распределения вероятности. Если, например, гистограмма имеет вид, показанный на рис. 34, а, то результат измерения определенно не подчиняется нормальному закону. Если же гистограмма имеет вид показанный на рис. 34, б, то возникает сомнение: достаточно ли хорошо она соответствует теоретической кривой нормального закона распределения нормальному закону. Если же гистограмма имеет вид показанный на рис. 34, б, то возникает сомнение: достаточно ли хорошо она соответствует теоретической кривой нормального закона распределения плотности вероятности, показанной пунктиром? Для разрешения этого сомнения нужно иметь правило, руководствуясь которым можно было бы принимать то или иное решение.

Существует несколько так называемых критериев согласия, по которым проверяются гипотезы о соответствии экспериментальных данных тому или иному закону распределения вероятности результата измерения. Наиболее распространенным из них является критерий К. Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения принимается сумма квадратов отклонения частностей  /п от теоретической вероятности
/п от теоретической вероятности  попадания отдельного
попадания отдельного
значения результата измерения в i-й интервал причем каждое слагаемое берется с коэффициентом п / 
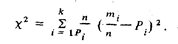
Если расхождение случайно, то  подчиняется
подчиняется  -распределению (хи - квадрат распределению К. Пирсона). Кривые интегральной функции этого распределения представлены на рис. 35*. Интегральная функция определяет вероятность того что случайное число примет значение, меньшее аргумента этой функции. Поэтому, задавшись значением интегральной функции распределения К. Пирсона F (
-распределению (хи - квадрат распределению К. Пирсона). Кривые интегральной функции этого распределения представлены на рис. 35*. Интегральная функция определяет вероятность того что случайное число примет значение, меньшее аргумента этой функции. Поэтому, задавшись значением интегральной функции распределения К. Пирсона F (  ), можно проверить больше или меньше ее аргумента
), можно проверить больше или меньше ее аргумента  (см. рис. 35) вычисленное значение
(см. рис. 35) вычисленное значение  . Если меньше, то выбранной вероятности c2 можно считать случайным числом, подчиняющимся
. Если меньше, то выбранной вероятности c2 можно считать случайным числом, подчиняющимся  - распределению К. Пирсона, т.е. признать, случайным расхождение между эмпирической и теоретической плотностью распределения вероятности результата измерения. Если же окажется, что
- распределению К. Пирсона, т.е. признать, случайным расхождение между эмпирической и теоретической плотностью распределения вероятности результата измерения. Если же окажется, что  >
>  то с той же вероятностью придется признать, что
то с той же вероятностью придется признать, что  не подчиняется распределению К. Пирсона т.е. гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается.
не подчиняется распределению К. Пирсона т.е. гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается.
*Здесь k соответствует числу интервалов только при проверке соответствия закона распределения вероятности результата измерения нормальному закону.

Пример 17.100 независимых числовых значений результата измерения напряжения цифровым вольтметром, каждое из которых повторилось m раз, приведены в первой графе табл. 9
Таблица 9
| U | m | mU | 
|  
| 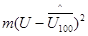
|
| 8,30 | 8,30 | -0,33 | 0,1089 | 0,1089 | |
| 8,35 | 16,70 | -0,28 | 0,0784, | 0,1568 | |
| 8,40 | 33,60 | -0,23 | 0,0529 | 0,2116 | |
| 8,45 | 42,25 | -0,18 | 0,0324 | 0,1620 | |
| 8,50 | 68,00 | -0,13 | 0,0169 | 0,1352 | |
| 8.55 | 85,50 | -0,08 | 0,0064 | 0,0640 | |
| 8,60 | 154,80 | -0,03 | 0,0009 | 0,0162 | |
| 8,65 | 147,05 | 0,02 | 0,0004 | 0,0068 | |
| 8,70 | 104.40 | 0,07 | 0,0049 | 0,0588 | |
| - 8,75 | 78,75 | 0,12 | 0,0144 | 0,1296 | |
| .8,80 | 61,60 | 0,17 | 0,0289 | 0,2023 | |
| 8,85 | 53,10 | 0,22 | 0,0484 | 0.2904 | |
| 8,90 | - | - | — | - | |
| 8,95 | 8,95 | 0.32 | 0,1024 | 0,1024 |
Проверить гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности.
Решение. 1. Используя результаты вспомогательных вычислений, приведенные в третьей графе, найдем среднее арифметическое значение результата изменения-

2. Используя результаты вспомогательных вычислений в четвертой, пятой и шестой графах, найдем стандартное отклонение результата измерения :

3. Ни одно из значений результата измерения не отличается от среднего арифметического больше чем на 3  = 0,381. Ошибок, следовательно, можно считать, что нет.
= 0,381. Ошибок, следовательно, можно считать, что нет.
4. При использовании критерия К. Пирсона в каждом интервале должно быть не меньше пяти независимых значений результата измерения. В соответствии с этим образуем интервалы так, как это представлено во второй графе табл. 10.
Таблица 10
| i |
Интервал

|

|
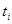
|

|

|

|
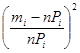
|
(  8,425) 8,425)
| -1,614 | -0,4467 | 0,0533 | 1,67 | 0,523 | ||
| (8,425;8,475) | -1,220 | -0,3888 | 0,0579 | -0,79 | 0,108 | ||
| (8.475;8,525) | -0,827 | -0,2959 | 0,0929 | 0,179 | |||
| (8,525;8,575) | -0,433 | -0,1676 | 0,1283 | -1,29 | 0,624 | ||
| (8,575;8,625) | -0.039 | -0,0156 | 0,1520 | -2,83 | 0,516 | ||
| (8,625;8,675) | 0,354 | 0,1383 | 0,1539 | 1,61 | 0,168 | ||
| (8,675;8,725) | 0,748 | 0,2728 | 0,1345 | -1,45 | 0,157 | ||
| (8,725;8,775) | 1,142 | 0.3733 | 0,1005 | -1,05 | 0,110 | ||
| (8,775;8,825) | 1,536 | 0,4377 | 0,0644 | 0,56 | 0,048 | ||
(8,825;+  ) )
| 
| .0,5000 | 0,0623 | 0,77 | 0,095 |
5. Определим, на сколько  и в каком направлении отстоит от среднего арифметического правая граница
и в каком направлении отстоит от среднего арифметического правая граница  , каждого интервала:
, каждого интервала:

Полученные значения параметра t (см. разд. 2.3.4) внесем в четвертую графу табл. 10.
6. По значению 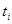 . из графика на рис. 22 можно определить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному, закону распределения вероятности, попадает в интервал
. из графика на рис. 22 можно определить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному, закону распределения вероятности, попадает в интервал  С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность, как показано в разд. 2.3.4 (формула 9), определяется интегралом вероятности - функцией Лапласа
С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность, как показано в разд. 2.3.4 (формула 9), определяется интегралом вероятности - функцией Лапласа  , так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения
, так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения  занесены в пятую графу табл. 10.
занесены в пятую графу табл. 10.
7. Теоретическая вероятность  попадания в i-й интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, очевидно равна
попадания в i-й интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, очевидно равна

Принимая во внимание, что  а
а 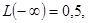 поместим рассчитанные значения
поместим рассчитанные значения  , в шестую графу табл. 10.
, в шестую графу табл. 10.
8. В седьмую и восьмую графу внесены результаты остальных вспомогательных вычислений. Суммирование чисел в восьмой графе дает
х2 = 2,528.
9. Из графика на рис. 35 видно, что рассчитанное значение  , соответствующего, например, вероятности 0,95. Таким образом можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.
, соответствующего, например, вероятности 0,95. Таким образом можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.
Критерий согласия К. Пирсона широко применяется для проверки гипотез о том, что результат измерения подчиняется вполне определенному закону распределения вероятности. При  соответствующая гипотеза принимается, при
соответствующая гипотеза принимается, при 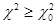 - отвергается. Однако даже вьполнение неравенства
- отвергается. Однако даже вьполнение неравенства  не может служить доказательством того, что результат измерения подчиняется этому закону распределения вероятности.
не может служить доказательством того, что результат измерения подчиняется этому закону распределения вероятности.
При использовании критерия К. Пирсона, как и в случае применения других критериев, возможны два рода ошибок. Ошибка первого рода состоит в отклонении верной гипотезы, а ошибка второго рода — в принятии неправильной. Для иллюстрации на рис. 36 показаны кривые плотности распределения вероятности величины  в случаях, когда проверяемая гипотеза верна — кривая 1, и когда неверна — кривая 2.
в случаях, когда проверяемая гипотеза верна — кривая 1, и когда неверна — кривая 2.

Если вероятности, с которой выносится решение, соответствует значение  , то при всех
, то при всех  гипотеза будет приниматься, а при всех
гипотеза будет приниматься, а при всех 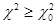 - отклоняться. Вероятности ошибок первого и второго рода при этом:
- отклоняться. Вероятности ошибок первого и второго рода при этом:

Обе они зависят от значения  , которое в свою очередь определяется вероятностью
, которое в свою очередь определяется вероятностью  , с которой принимается решение. С повышением этой вероятности значение
, с которой принимается решение. С повышением этой вероятности значение  увеличивается, вероятность ошибки первого рода уменьшается, а ошибки второго рода — возрастает, и наоборот. Таким образом, нецелесообразно принимать решение с очень высокой степенью вероятности. Обычно Р выбирается равной 0,9 . . . 0,95.
увеличивается, вероятность ошибки первого рода уменьшается, а ошибки второго рода — возрастает, и наоборот. Таким образом, нецелесообразно принимать решение с очень высокой степенью вероятности. Обычно Р выбирается равной 0,9 . . . 0,95.
При проверке нормальности закона распределения вероятности результата измерения применение критерия К. Пирсона дает хорошие результаты только, если п > 40 ... 50. При 10 ... 15 < п < 40 ... 50 применяется так называемый составной критерий. Сначала рассчитывается

и проверяется выполнение условия

где  и
и  зависят от вероятности Р*, с которой принимается решение, и находятся по табл. 11.
зависят от вероятности Р*, с которой принимается решение, и находятся по табл. 11.
Таблица 11
| n | Р*= 0,90 | Р* = 0,95 | .Р*=0,99 | |||

| 
| 
| 
| 
| 
| |
| . 11 16 21 26 31 36 41 46 51 | 0,7409 7452 7495 7530 7559 7583 7604 7621 7636 | 0,8899 8733 | 0,7153 7236 7304 7360 7404 7440 7470 7496 7518 | 0,9073 8884 | 0,6675 6829 | 0,9359 9137 |
Если это условие соблюдается, то дополнительно проверяются "хвосты" теоретического и эмпирического законов распределения вероятности. При 10  20 считается допустимым отклонение одного из независимых значений результата измерения
20 считается допустимым отклонение одного из независимых значений результата измерения  , от среднего арифметического больше чем на 2,5 Sq , при 20 < к < 50 — двух, что соответствует доверительной вероятности P**
, от среднего арифметического больше чем на 2,5 Sq , при 20 < к < 50 — двух, что соответствует доверительной вероятности P**  0,98.
0,98.
Несоблюдения хотя бы одного из двух условий достаточно для того, чтобы гипотеза о нормальности закона распределения вероятности результата измерения была отвергнута. В противном случае гипотеза принимается с вероятностью Р  Р* +Р**-1.
Р* +Р**-1.
При п < 10 ... 15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется. Решение принимается на основании анализа априорной информации.
2.6.3. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ, ПОДЧИНЯЮЩИХСЯ НОРМАЛЬНОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ
Если итоги проверки большого массива экспериментальных данных по критерию  не противоречат гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности, то можно считать, что среднее арифметическое значение результата измерения также подчиняется нормальному закону (см. рис. 32), а среднее значение среднего арифметического (см. разд. 2.6.1)
не противоречат гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности, то можно считать, что среднее арифметическое значение результата измерения также подчиняется нормальному закону (см. рис. 32), а среднее значение среднего арифметического (см. разд. 2.6.1)

Как было показано в разд. 2.3.4, ни одно из случайных значений, подчиняющихся нормальному закону распределения вероятности, не может отличаться от среднего значения больше чем на половину доверительного интервала. На основании формулы (9) можно написать

Заменяя среднее квадратическое отклонение среднего арифметического его оценкой

вытекающей из выражения (11), и принимая во внимание,
что, как показано в разд. 2.4, 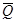 = Q, получим:
= Q, получим:

где  - половина доверительного интервала, a t при выбранной доверительной вероятности определяется по верхней кривой на рис. 22.
- половина доверительного интервала, a t при выбранной доверительной вероятности определяется по верхней кривой на рис. 22.
Порядок соответствующих действий показан на рис. 33. Сначала находится стандартное отклонение среднего арифметического, затем выбирается доверительная вероятность и определяется соответствующее ей значение t по верхней кривой на рис. 22. С выбранной доверительной вероятностью значение измеряемой величины Q не отличается от среднего арифметического значения результата измерения больше, чем на половину доверительного интервала 
При небольшом объеме экспериментальных данных среднее арифметическое значение результата измерения, подчиняющегося нормальному закону распределения вероятности, само подчиняется закону распределения вероятности Стъюдента (псевдоним B.C. Госсета) с тем же средним значением , 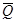 = Q . Графики плотности распределения вероятности, соответствующие этому закону, показаны на рис. 37. При увеличении п распределение вероятности Стьюдента быстро приближается к нормальному, становясь почти неотличимым от него уже при п > 40 ... 50.
= Q . Графики плотности распределения вероятности, соответствующие этому закону, показаны на рис. 37. При увеличении п распределение вероятности Стьюдента быстро приближается к нормальному, становясь почти неотличимым от него уже при п > 40 ... 50.
Доверительная вероятность того, что любое случайное значение среднего арифметического, подчиняющегося закону распределения вероятности Стьюдента, не отличается от соседнего значения больше, чем на половину доверительного интервала,

где  (t) — интегральная функция распределения вероятности Стьюдента. По этой формуле на рис. 38 построены графики, показывающие, какое значение имеет объем выборки п. При п = 4, например, вероятность того, что никакое значение среднего арифметического, подчиняющегося закону распределения вероятности Стьюдента, не отличается от среднего значения больше чем на, 2
(t) — интегральная функция распределения вероятности Стьюдента. По этой формуле на рис. 38 построены графики, показывающие, какое значение имеет объем выборки п. При п = 4, например, вероятность того, что никакое значение среднего арифметического, подчиняющегося закону распределения вероятности Стьюдента, не отличается от среднего значения больше чем на, 2  , составляет 0,86; при п = 6 она равна 0,9; при п = 10 получается равной 0,924; при п = 20 уже 0,94 и т.д. Верхняя кривая на рис. 38 соответствует условию п > 40 ... 50 и практически не отличается от верхней кривой на рис. 22.
, составляет 0,86; при п = 6 она равна 0,9; при п = 10 получается равной 0,924; при п = 20 уже 0,94 и т.д. Верхняя кривая на рис. 38 соответствует условию п > 40 ... 50 и практически не отличается от верхней кривой на рис. 22.
По аналогии с предыдущим нетрудно показать, что
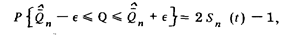

|

где по-прежнему  — половина доверительного интервала, а г при выбранной доверительной вероятности определяется по графику на рис. 38.
— половина доверительного интервала, а г при выбранной доверительной вероятности определяется по графику на рис. 38.
Порядок действий при обработке небольшого объема экспериментальных данных отличается только тем, что после выбора доверительной вероятности t с учетом п определяется по графику на другом рисунке.
При совсем незначительном количестве экспериментальных данных (  10 ... 15) и принятой гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности, выявление ошибок по - правилу трех сигм" не производится. Остальной порядок действий (см. рис. 33) не отличается от предыдущего. Доверительный интервал при фиксированной доверительной вероятности, как это видно из графика на рис. 38, с уменьшением объема экспериментальных данных расширяется; точность измерения, следовательно, снижается, приближаясь к точности однократного измерения, при
10 ... 15) и принятой гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности, выявление ошибок по - правилу трех сигм" не производится. Остальной порядок действий (см. рис. 33) не отличается от предыдущего. Доверительный интервал при фиксированной доверительной вероятности, как это видно из графика на рис. 38, с уменьшением объема экспериментальных данных расширяется; точность измерения, следовательно, снижается, приближаясь к точности однократного измерения, при  .
.
Дата добавления: 2015-02-10; просмотров: 327; Мы поможем в написании вашей работы!; Нарушение авторских прав |