Решение. 1. Согласно условию

Критерии, приводящие к отношению правдоподобия. Обозначим через P_N вероятность то­го, что сигнал на выходе оптимального фильтра представляет собой только реакцию на помеху, а через P_X+N — вероятность того, что в нем содержится еще и отклик на полезный входной сигнал. Тогда вероятность ошибочного решения

Естественно, что условный „идеальный наблюдатель", прини­мающий решения, либо вообще не должен совершать ошибок, либо должен свести до минимума их вероятность. Поэтому критерий

называется критерием идеального наблюдателя. Он является частным случаем критерия минимума среднего риска, в ко­тором учитывается значимость или стоимость ошибок каж­дого вида:

Заменяя P_Iна 1 — P₀ и выполняя преобразования, тот и другой критерии можно представить в общем виде:

Последнее выражение минимизируется при

что вполне понятно, так как вероятность правильного обнару­жения желательно иметь возможно большую, а вероятность ложной тревоги возможно меньшую.

Полученное выражение может рассматриваться самостоя­тельно и называется критерием взвешенной (с помощью g) комбинации (из двух слагаемых).

Для того, чтобы вывести из критерия взвешенной комби­нации значение W_opt введем в рассмотрение функцию решения

с помощью, которой выражения для вероятности правильного обнаружения и вероятности ложной тревоги запишутся в виде:

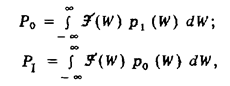
где значения интегралов на участке изменения переменной от — ∞ до неоптимального пока еще порога W₀ равны нулю.

Критерий взвешенной комбинации можно тогда представить в виде

p₀ (W) F(W) (L - g) dW = max,

где L = 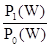называется отношением правдоподобия.

В подынтегральном выражении с порогом обнаружения связа­на только функция решения. Следовательно, максимизиро­вать интеграл можно только за счет выбора этой функции. Но она имеет всего два значения: 0 и 1. Поэтому поступим следующим образом. Принимая во внимание, что плотность распределения вероятностиp₀ (W) всегда положительна, будем придавать функции решения F(W) значение 0, если раз­ность L — g отрицательная, и значение 1, если эта разность положительная. В этом случае, очевидно , значение интеграла

будет максимальным, а оптималь­ное правило решения запишется в виде

ì0 при L£g

F_opt (W) í

î1 при L>g

Дальнейшее зависит от того, что представляет собой отноше­ние правдоподобия. С одной сто­роны; как отношение двух плотностей вероятности оно не может быть отрицательным. С другой стороны; конкретный его вид зависит от законов распределе­ния вероятности сигнала на выходе оптимального фильтра при наличии и при отсутствии в нем отклика на полезный входной сигнал. Таким образом, в отличие от синтеза оп­тимального порога обнаружения по критерию Неймана — Пирсона здесь требуется знание р₁ (W) в реальных условиях эксплуатации. На практика обычно корректируют порог по мере накопления необхо­димых сведений, либо задаются мо­делью сигнала на этапе проекти- рования средства измерений.

Пример 48. Реакция оптимального фильтра на помеху подчиняется нормированному нормальному закону распределения вероятности, а от­клик на полезный входной сигнал равен 1. Определить оптимальный порог обнаружения при заданном значении у.

Решение. Отношение правдоподобия

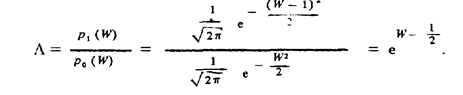
График этой функции построен на рис. 97, а. При L g оптимальная функ­ция решения F_opt (W) = 0, и принимается решение, что полезного сигнала нет. При L > g Оптимальная функция решения F_opt(W) = 1 принимается решение, что полезный сигнал есть (см. рис. 97, б) : Отсюда

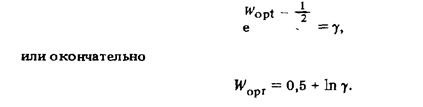
Теория статистических решений используется также при конт­роле.

* В примерах 24. . .28 предполагается, что остальными факторами, влияющими на результат измерения, можно пренебречь.