
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
TERMINATE 2 страница. информационную базу данных объекта;
 информационную базу данных объекта;
информационную базу данных объекта;
 выражение целевой функции как математическое представление критерия оптимальности через отобранные экономические показатели, с обозначением экстремума целевой функции (максимум или минимум);
выражение целевой функции как математическое представление критерия оптимальности через отобранные экономические показатели, с обозначением экстремума целевой функции (максимум или минимум);
 представление системы ограничений математически в виде уравнений, неравенств через другие экономические показатели.
представление системы ограничений математически в виде уравнений, неравенств через другие экономические показатели.
Необходимо отметить, что одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.
Методика построения экономико-математических моделей состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения.
Все условия задачи необходимо записать в виде уравнений или неравенств. В первую очередь необходимо определить систему переменных величин, которые для конкретной задачи могут обозначать искомый объем производства продукции на предприятии, количество перевозимого груза определенным потребителям и т.д. Как правило, для обозначения переменных величин используются буквы: x, y, z, а также их модификации. Например, модификации переменной x: x1, x2, xn и т.д.
Переменные x1, x2, …., xn могут обозначать объемы производства продукции соответственно первого, второго и так далее n-го вида. Переменная  может обозначать объемы производства j-го вида продукции на i-ом виде оборудования по s-му технологическому способу.
может обозначать объемы производства j-го вида продукции на i-ом виде оборудования по s-му технологическому способу.
Для индексации, как правило, используются латинские буквы: i, j, s, l. Количество значений переменных может обозначаться буквами n, k, m. По каждой переменной для конкретной задачи дается словесное пояснение.
Целевую функцию задачи чаще обозначают буквами f, F, Z. Постоянные величины (нормы затрат ресурсов, цена или прибыль от единицы продукции и др.) обычно обозначают буквами: a, b, c, d и т.д.
Математическую модель задачи можно представить в виде:
найти значения переменных x1, x2,…., xn, которые максимизируют или минимизируют целевую функцию
 (1.1)
(1.1)
и удовлетворяют системе из m ограничений
 . (1.2)
. (1.2)
Если на переменные накладываются условие неотрицательности, тогда в модель задачи вводится условие
 . (1.3)
. (1.3)
Иногда на переменные налагается условие целочисленности, тогда его можно записать в виде
xj = 0, или 1, или 2, или 3 и т.д.
Если ограничения (1.2) и целевая функция (1.1) линейны относительно переменных, то модель называется линейной. В случае если хотя бы одна из функций (1.2) или Z нелинейна, то модель называется нелинейной.
Модель общей задачи линейного программирования применяют для решения задач определения оптимального плана выпуска продукции, оптимального использования производственных мощностей, сырья и других задач. В каждой из них отыскивается оптимум целевой функции при линейных ограничениях.
Задачи оптимизации решаются путём применения оптимизационных моделей методами линейного программирования.
Вопросы по теме.
1. Различие между параметрами и переменными в оптимизационной модели.
2. Назовите составные части оптимизационной модели.
3. В чем различие между понятиями критерий оптимальности и целевая функция.
4. Представьте запись общей модели оптимизационной задачи.
5. Приведите пример, подтверждающий, что одной системе ограничений может соответствовать несколько критериев оптимальности.
1.7 Основные этапы становления и развития школы экономико-математического моделирования.
Родоначальником экономико-математического моделирования является Франсуа Кэне (1694-1774), который впервые использовал балансовый метод для имитации динамики внешней торговли и создания первой в мире модели народного хозяйства. В 1758г. был опубликован первый вариант «экономической таблицы», которая представляла собой схему процесса расширенного воспроизводства. Однако модели Кэне носили чисто количественный характер и были эффективны для анализа, а не для принятия решений, внутренняя природа явлений автором не рассматривалась.
В дальнейшем идеи Кэне получили свое развитие в 2-х самостоятельных экономических концепциях:
· концепция экономико-математического моделирования хозяйственных процессов при помощи межотраслевого баланса;
· получила развитие теория, связанная с дифференциацией экономических систем на производство средств производства и предметов потребления, а также в трендовом моделировании рынка средств производства.
Рассмотрим вклад известных ученых-экономистов в развитие школы экономико-математического моделирования.
Леон Вильрас (1874-1877гг) впервые в чистом виде применил математику для описания экономических процессов. Однако он не учитывал объективность законов хозяйственного развития, опираясь исключительно на арифметический подход. Как следствие – многие его модели оказались невостребованными.
Вильфред Паретто (1848-1923гг.) впервые применил теорию вероятности для моделирования экономических процессов; разработал ряд статистических моделей соотношения доходов разных групп населения. Основное достоинство этих моделей состоит в том, что они носили оптимизационный характер, т.е. при помощи последовательности расчетов можно определить состояние и соотношение доходов, при котором состояние хозяйственной системы будет оптимальным. В экономической науке широко используется термин «оптимум по Паретто», который означает сглаживание уровней доходов для уменьшения разрыва между наиболее высокооплачиваемой частью и наименее низкооплачиваемой частью населения.
Альфред Маршалл (1842-1924гг.) впервые использовал графические модели для объяснения природы экономических процессов.
Джон Мейнар Кейнс (1883-1943гг.) на основе использования экономико-математических моделей пришел к выводу о возможности выявления основных сфер, инструментов управления экономической системой и достижения экономикой оптимального состояния с помощью государственного регулирования. Он разработал экономико-математическую модель функционирования экономики в условиях полной занятости. Этот подход состоял в основе экономической политики государств почти до 70-х годов ХХ века.
Во второй половине ХХ века существовал подход, в соответствии с которым выделялись три этапа развития экономико-математического моделирования: математическая школа; статистическое направление; эконометрика[1].
Существенный вклад в развитие школы экономико-математического моделирования внесли отечественные ученые.
С конца 19 века оригинальные экономико-математические исследования проводились В.К.Дмитриевым, В.И.Борткевичем, В.В.Самсоновым, которые находились под сильным влиянием психологической школы, рассматривавшей экономические явления как результаты психологических реакций хозяйствующих субъектов.
В.К.Дмитриев (1868-1913гг.) построил модель полных затрат труда и сбалансированных цен в виде системы линейных уравнений с технологическими коэффициентами. В отличие от теоретиков западной математической школы, В.К.Дмитриев занимался и прикладными статистическими исследованиями.
Н.Д. Кондратьев (1892-1938гг.) впервые использовал функциональный метод анализа для моделирования экономических процессов. Разработанная им теория «больших конъюнктурных циклов», опубликованная в 1925-1928 гг., позволила определить влияние одних хозяйственных секторов на другие и оценить временной лаг, который необходим хозяйственным секторам для приспособления к происходящим переменам.
После революции, в 20-е годы ХХ века, в нашей стране развивались два основных направления: моделирование процесса расширенного воспроизводства и применение методов математической статистики в изучении хозяйственной конъюнктуры и в прогнозировании.
Выдающимся достижением советской статистики стала разработка первого в мире баланса народного хозяйства СССР за 1923/1924 хозяйственный год. Позднее проводились работы по совершенствованию статистических основ межотраслевого баланса.
Значительной вехой в истории экономических исследований стала разработка Г.А.Фельдманом (1884-1958гг.) математических моделей экономического роста, основанных на схемах расширенного воспроизводства К.Маркса. Основная модель роста Г.А.Фельдмана выражала взаимосвязи темпов роста национального дохода, изменения фондоотдачи и производительности труда, структуры использования национального дохода.
Другое направление экономико-математических исследований 20-х годов ХХ века было представлено многочисленными работами по анализу хозяйственной конъюнктуры, анализу временных рядов и сезонных колебаний, краткосрочным экономическим прогнозам на основе математико-статистических моделей.
Позднее, в 1938-1939 гг. Л.В.Канторович сформулировал новый класс условно-экстремальных задач и предложил методы их решения – позже эта область прикладной математики получила название «линейное программирование».
Л.В.Канторович (1912-1986гг.) не только является автором линейного программирования, он также разработал порядок его использования для решения практических задач управления. Л.В.Канторович доказал, что большинство задач оперативного планирования промышленного предприятия могут быть сведены к задачам линейного программирования; при помощи совокупности математических преобразований можно найти оптимальный вариант, который при наименьших затратах ресурсов обеспечит наибольший результат. В 1975 г. Л.В.Канторович стал лауреатом Нобелевской премии.
Выдающуюся роль в создании отечественной экономико-математической школы сыграл В.С.Немчинов (1894-1964). В 60-е годы ХХ века были разработаны важные теоретические положения: проблемы народно-хозяйственного оптимума, соизмерения затрат и результатов, закономерностей расширенного воспроизводства, структурного анализа экономической системы.
Моделирование экономических систем осуществлялось в различных областях: народно-хозяйственного моделирования, моделирования отраслей производства и территориальных систем, а также моделирования планирования и управления на предприятиях.
В настоящее время экономико-математическое моделирование является одним из приоритетных направлений развития экономического анализа на базе использования новейших достижений математических методов и вычислительной техники.
Вопросы по теме.
1. Назовите автора первой экономико-математической модели.
2. Назовите имена наиболее видных зарубежных ученых-экономистов, внесших весомый вклад в развитие экономико-математического моделирования.
3. Назовите имена наиболее видных отечественных ученых-экономистов, внесших весомый вклад в развитие экономико-математического моделирования.
4. Назовите российских экономистов, работавших в области экономико-математического моделирования, ставших лауреатами нобелевской премии.
Раздел II Экономико-математические модели планирования и анализа производственно-хозяйственной деятельности предприятия.
В современных условиях выбор оптимальных вариантов планирования и управления производством представляет серьезную проблему. В рыночных условиях проявляется жесткая конкуренция товаропроизводителей внутри страны, а также усиливаются потоки товаров, услуг и капиталов из зарубежных стран. Поэтому нельзя принять обоснованные решения без переработки большого количества информации, характеризующей эффективность использования трудовых, материальных и денежных ресурсов. Такая задача может быть решена только с использованием ЭВМ и соответствующих экономико-математических моделей и методов. На уровне промышленных предприятий накоплен немалый опыт решения экономических задач, результаты которых успешно используются в целях планирования и управления. К ним относятся модели формирования производственной программы предприятия, оптимального использования производственных мощностей, оптимизации технологической подготовки производства (модели раскроя промышленных материалов, составления смесей) и др. В настоящее время мощности современных доступных ЭВМ и стандартное программное обеспечение позволяют реализовать эти модели на любом предприятии, фирме.
2.1 Экономико-математические модели составления производственной программы предприятия.
Рассмотрим методологические и методические вопросы составления портфеля заказов предприятия в применении к простым по экономическому содержанию моделям и методам.
2.1.1Пример составления экономико-математической модели задачи формирования производственной программы предприятия.
Постановка задачи: цех выпускает три вида изделий, производственные возможности цеха характеризуются следующими данными:
- суточный фонд времени работы оборудования 780 часов;
- суточный расход сырья 850 тонн;
- суточный расход электроэнергии 790 квт-час.
Нормы затрат производственных ресурсов на единицу различных изделий приведены в таблице 2.1:
Таблица 2.1
| Ресурс | Ед. изм. | Изделия, расход ресурса на производство одного изделия | Суточный лимит (запас ресурса) | ||
| X1 | X2 | X3 | |||
| Оборудование | часы | ||||
| Сырье | тонны | ||||
| Электроэнергия | квт-час | ||||
| Оптовая цена | тыс.руб |
Составить план производства, обеспечивающий максимальный объем выпуска продукции в стоимостном выражении.
Запись условия задачи в виде представленной таблицы 2.1 с объяснением данных является экономической моделью задачи.
Математическая модель задачи может быть представлена в следующем виде:
Пусть х1, х2 и х3 – искомые объемы выпуска 1-го, 2-го и 3-его видов изделий.
Требуется найти неотрицательные значения переменных х1, х2 и х3, обеспечивающих максимальный по стоимости выпуск продукции.
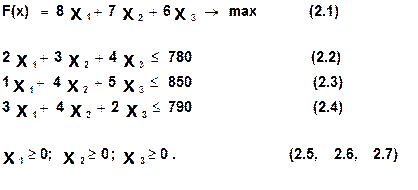
Совокупность выражений (2.1)÷(2.7) представляет собой математическую модель задачи.
Математическая модель задачи выражений состоит из критерия оптимальности (2.1) и системы ограничений (2.2)÷(2.7). В последней можно выделить ограничение неотрицательности (2.5)÷(2.7), показывающее, какие значения могут принимать переменные., а также основные ограничения (2.2)÷(2.4), указывающие, какие преобразования можно проводить с переменными. Система ограничений определяет множество допустимых значений переменных, из которых с помощью критерия оптимальности и отыскиваются наилучшие (по данному критерию) значения.
Запишем экономико-математическую модель рассмотренной задачи в общем виде, т.е. в символах.
Введем обозначения:
 индекс ресурсов (
индекс ресурсов (  = 1, 2, ….,
= 1, 2, ….,  );
);
 индекс изделия (
индекс изделия (  = 1, 2, ….,
= 1, 2, ….,  );
);
 наличный объем
наличный объем  -го ресурса;
-го ресурса;
 норма затрат
норма затрат  -го ресурса на производство единицы
-го ресурса на производство единицы  -го
-го
изделия;
 оптовая цена единицы изделия
оптовая цена единицы изделия  -го вида;
-го вида;
 искомый объем производства
искомый объем производства  -го изделия.
-го изделия.
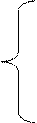
В данных обозначениях задача запишется следующим образом.
Найти значения переменных  , максимизирующие целевую функцию вида
, максимизирующие целевую функцию вида


при выполнении ограничений на использование ресурсов:

и неотрицательности переменных:


Выражение (2.8) максимизирует совокупный эффект от всего объема выпущенных изделий всех видов. Выражение (2.9) означает, что для любого из ресурсов его суммарный расход на производство изделий всех видов не превосходит всего имеющегося объема (выделенного лимита). Левая часть выражения показывает используемый в оптимальном плане обьем i-го ресурса, а правая часть имеющийся обьем этого же ресурса. Выражение (2.10) означает неотрицательность выпусков изделий.
Особенность экономико-математической модели (2.8)÷(2.10) состоит в том, что она справедлива для любого количества видов продукции и ресурсов, для самых разнообразных численных значений лимитов ресурсов и норм затрат ресурсов. Коэффициенты при неизвестных в целевой функции означают эффективность от выпуска единицы продукции (прибыль, цена).
Таким образом, экономико-математическая модель (2.8)÷(2.10) соответствует любой экономической задаче по отысканию максимума эффекта от выпуска продукции при ограничениях на количество используемых ресурсов (при условии линейной зависимости эффекта и использования ресурсов от объема выпуска).
Задача формирования производственной программы может быть поставлена и на минимум целевой функции. Например, необходимо
отобрать в план такие изделия, чтобы суммарные затраты на изготовление продукции были минимальными. Если принять, что  ─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:
─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:
 (2.11)
(2.11)
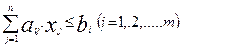 (2.12)
(2.12)
 (2.13)
(2.13)
Для модели такого вида существует простое оптимальное решение все неизвестные равны нулю. Действительно, при 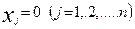 все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
В этой упрощенной модели не учтена цель производства получение результата в виде конечной продукции, а в процессе производства необходимо сопоставление затрат и результатов. Очевидно, необходимо ввести дополнительное ограничение, которое позволило бы не сводить к нулю затраты. В данном случае задача должна быть поставлена следующим образом: минимизация затрат при фиксированном уровне результата.
Рассмотрим экономико-математическую модель задачи на минимум затрат при фиксированных планах производства.
 (2.14)
(2.14)
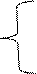
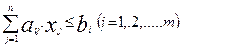 (2.15)
(2.15)
 (2.16)
(2.16)
Но любой сверхплановый выпуск увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при  , а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором
, а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором  .
.
Ограничить минимум затрат снизу можно при другой постановке задачи. Пусть  цена на продукцию
цена на продукцию  -го вида, а
-го вида, а  план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:
план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:
 (2.17)
(2.17)

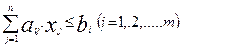 (2.18)
(2.18)
 (2.19)
(2.19)
 (2.20)
(2.20)
Постановка задачи на минимум затрат имеет смысл и в том случае, если существует несколько способов производства одноименной продукции. Например, изделия проходят обработку на токарных станках, но рабочими разной квалификации, или с использованием разных технологических способов (приспособлений). В модели
 (2.21)
(2.21)
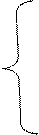
 (2.22)
(2.22)
 (2.23)
(2.23)
 (2.24)
(2.24)
плановое задание по выпуску продукции  осуществляется подбором разных величин
осуществляется подбором разных величин  , для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
, для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
2.1.2 Экономическая интерпретация результатов решения задачи формирования портфеля заказов
Для решения задач линейного программирования существует универсальный метод – симплекс-метод, который может быть, в частности, реализован в EXCEL с помощью надстройки «Поиск решения». Важное значение имеет не только решение с целью получения вычисленных значений переменных, но и анализ полученных результатов и устойчивость найденного решения к возможным изменениям внутренних и внешних условий. Рассмотрим интерпретацию результатов реализации в ЕXCEL задачи формирования производственной программы на примере модели (2.8)÷(2.10).
Основные результаты решения задачи содержатся в двух отчетах: отчете по результатам и отчете по устойчивости (оба отчета представлены на рис. 2.1).
В отчет по результатам, состоящий из трех небольших таблиц, включаются конечные значения целевой функции и переменных, дополнительные сведения об ограничениях.
В отчете по устойчивости (состоит из двух маленьких таблиц) содержатся сведения о чувствительности полученного решения к малым изменениям коэффициентов целевой функции или в формулах ограничений.
Выводы по отчету по результатам. Оптимальным планом предусматривается выпуск только двух видов изделий: 1-го и 3-го вида в количестве 200 и 95 единиц соответственно.

Рис. 2.1 Содержимое отчетов, созданных по результатам решения задачи в EXCEL.
При таком плане общая стоимость выпущенной продукции будет максимальной и составит 2170 тыс.руб. При этом фактическое использование ресурсов составит: по оборудованию – 780 часов, по сырью – 675 тонн, а по электроэнергии –790 квт-часов, т.е. ресурсы оборудования и электроэнергии используются полностью, а сырье недоиспользуется в объеме 175 тонн.
Выводы по отчету по устойчивости. Табличка «Изменяемые ячейки» содержит помимо результата решения задачи (колонка «Результирующее значение») нормированную стоимость единицы каждого вида изделия. Нормированная стоимость показывает, на какую величину изменится значение критерия оптимальности при увеличении объема выпуска данной продукции на одну единицу. Поскольку критерий (целевая функция) в данной задаче на максимум - то отрицательное значение теневой цены характеризует невыгодность продукции; если же теневая цена положительна то соответствующая продукция выгодна. Невыгодной к выпуску является 2-ой вид изделия, выпуск каждой единицы 2-го изделия приведет к снижению значения целевой функции на 3,75 тыс.руб., поэтому выпуск этого вида изделия оптимальным планом не предусмотрен.
Три последних колонки содержат значение коэффициентов целевой функции (оптовая цена единицы каждого вида продукции) и предельные значения приращения целевых коэффициентов, при которых сохраняется найденное оптимальное решение. Например, допустимое увеличение цены на изделие 2-говида равно 3,75 тыс. руб/единицу, а допустимое уменьшение практически неограниченно. Это означает, что если цена изделия второго вида вырастет более чем на 3,75 тыс. руб./единицу, то оптимальное решение изменится: станет целесообразным выпускать второй вид изделия. А если цена этого изделия будет снижаться вплоть до нуля, то оптимальное решение (200, 0, 95) останется прежним.
Во второй части отчета по устойчивости содержится информация, относящаяся к ограничениям. В колонке «Результирующее значение» повторяется объемы использованных ресурсов. В следующей колонке приводится значение теневой цены (двойственной оценки) каждого из ресурсов. Теневая цена показывает ценность дополнительной единицы ресурса и показывает, на сколько изменится значение критерия оптимальности при увеличении количества данного ресурса на одну единицу. Чем больше значение теневой цены, тем более дефицитен ресурс, тем больше возрастает критерий оптимальности при увеличении этого ресурса на одну единицу. Теневая цена рассчитывается только для дефицитных видов ресурсов. Дефицитные ресурсы используются в оптимальном плане полностью. В нашей задаче ресурсы оборудование и электроэнергия имеют отличные от нуля теневые цены 0,25 и 2,5 эти ресурсы используются полностью и поэтому являются дефицитными. Ограниченное количество оборудования и электроэнергии является сдерживающим фактором при оптимизации производственной программы: увеличение этих видов ресурсов привело бы к более хорошему варианту оптимального плана – за счет производства большего объема продукции и суммарная стоимость была бы больше.
Сырье полностью не используется в оптимальном плане, этот ресурс не является дефицитным и его увеличение не влияет на план выпуска продукции, поэтому его теневая цена равна нулю. Недефицитность ресурса возникает из-за невозможности его полного использования в полученном оптимальном плане. Суммарный расход сырья в количестве 675 тонн меньше его общего количества 850 тонн, поэтому план производства этим видом ресурса не лимитируется, Рассчитаем коэффициент использования сырья путем деления фактически используемого в оптимальном плане сырья на объем сырья, имеющегося в наличии: К=675/850=79,4%.
Необходимо отметить, что теневые цены ресурсов нельзя отождествлять с действительными ценами при закупке ресурсов. Теневая цена ресурса характеризует ценность ресурса относительно полученного оптимального решения.
Значения трех последних колонок (значение правой части ограничения, допустимое увеличение и допустимое уменьшение правой части) определяют диапазон изменения запасов ресурсов, в пределах которого можно рассчитать другие оптимальные решения, но сама структура оптимального плана не меняется (изделия, которые были убыточны, по-прежнему не будут входить в новые планы), а значения двойственных оценок ресурсов сохраняются.
Дата добавления: 2014-11-13; просмотров: 348; Мы поможем в написании вашей работы!; Нарушение авторских прав |