
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
TERMINATE 3 страница. По дефицитному ресурсу, который используется полностью, можно определить – на сколько нужно увеличить его объем для получения другого оптимального решения
По дефицитному ресурсу, который используется полностью, можно определить – на сколько нужно увеличить его объем для получения другого оптимального решения, которое было бы более хорошим по сравнению с рассматриваемым, т.е. обеспечило бы получение большей прибыли.
Например, в рассматриваемом примере дефицитным ресурсом является электроэнергия, в оптимальном плане этот ресурс используется полностью – все 790 квт-час. При увеличении лимита электроэнергии на 100 квт-час может быть получено более хорошее оптимальное решение, поскольку можно будет произвести больше продукции и увеличить общую стоимость произведенной продукции.
Однако, если получить дополнительно 400 квт-час электроэнергии, то электроэнергия в количестве 400-380=20 квт-час останется неиспользованной.
Если же ресурс является недефицитным и используется в оптимальном плане не полностью, то по данному ресурсу допустимое увеличение не определяется, а допустимое уменьшение определяется как разность между имеющимся объемом ресурса и фактически используемым его объемом.
Результаты решения моделей оптимизации производственной программы могут быть использованы для решения конкретных практических задач. Например, определить, какие виды продукции нерентабельны или какому ресурсу следует отдать предпочтение при решении задачи предельного увеличения запаса ресурсов.
Для того, чтобы изделие вошло в оптимальный план, его цена должна быть равна суммарной стоимости ресурсов, которые затрачены на производство единицы изделия, рассчитанной по двойственной оценке ресурсов. Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности (в нашей задаче это изделия первого и и третьего видов). Если стоимость ресурсов, затраченных на производство одного изделия, больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности.
Так, для производства единицы второго изделия используется 3 ед. ресурса оборудования, 4 ед. ресурса сырье и 4 ед. ресурса электроэнергия. Отвлечение 1 ед. дефицитного ресурса ведет к уменьшению критерия оптимальности на величину двойственной оценки.
Тогда производство единицы второго вида продукции ведет в целом к снижению критерия оптимальности на 3 ´0,25 + 4´0+ 4´2,5=10,75. Это больше, чем цена на единицу второго изделия на (10,75-7)=3,75. Таким образом, производство второго изделия нерентабельно, т.к. затраты ресурсов на него больше цены на 3,75 ед. Эта величина приведена в колонке «нормируемая стоимость» стандартной распечатки по результатам решения. При принудительном выпуске единицы нерентабельной продукции второго вида критерий оптимальности снизится на величину нормируемой стоимости – т.е. на 3,75 тыс.руб.
Сравним суммарную стоимостную оценку ресурсов, используемых при производстве единицы первого и третьего изделий, с их ценой.
По первому изделию: 2 ´0,25 + 1´0+ 3´2,5 =8= (8 тыс руб. цена первого изделия);
По третьему изделию: 4 ´0,25 + 5´0+2´2,5 =6=(6 тыс.руб. цена третьего изделия).
Таким образом, суммарная стоимостная оценка ресурсов, используемых при производстве единицы каждого из изделий первого и третьего вида, равна их цене, это рентабельные виды продукции, поэтому они включены в оптимальный план.
Перейдем к ответу на вопрос, какому ресурсу следует отдать предпочтение при решении задачи предельного увеличения запаса ресурсов.
При решении задачи предельного увеличения запаса ресурсов с целью максимизации выпуска продукции предпочтение следует отдать ресурсу, увеличение которого обеспечивает максимальный рост значения критерия оптимальности. Так, увеличение дефицитного ресурса электроэнергия на 1 квт-ч. приводит к росту критерия оптимальности на 2,5 тыс. руб.. Максимально (предельно) электроэнергию можно увеличить на 380 квт-ч., что приведет к росту критерия оптимальности на 2,5х380=950 тыс.руб. По оборудованию – 0,25х107,69=26,92 тыс. руб. Следовательно, руководству цеха выгодно добиться увеличения лимита на электроэнергию на 380 квт-ч.
2.1.3 Возможные критерии оптимальности и виды ограничений.
Важнейшей частью построения оптимизационной модели формирования портфеля заказов предприятием или фирмой являются обоснование и выбор в качестве критерия оптимальности того или иного экономического показателя, подлежащего оптимизации. Чаще всего в качестве критериев оптимальности в таких моделях используются следующие показатели:
· прибыль;
· объем реализации;
· объем добавленной стоимости;
· трудоемкость изготовления продукции;
· объем товарной продукции.
Каждый из приведенных выше показателей обладает определенными, свойственными только ему преимуществами и недостатками. До настоящего времени среди экономистов дискуссируется вопрос о согласовании показателей оценки эффективности функционирования предприятия с целью выработки единого критерия, объективно отражающего уровень эффективности производства. Большинство экономистов в настоящее время считают, что для оценки эффективности функционирования предприятия необходимо использовать систему показателей, с разных сторон характеризующих его деятельность. Соответствующие экономико-математические модели приобретают в этом случае многоцелевой характер. Существуют специальные методы решения многоцелевых задач, например, выбор одного локального критерия оптимальности и перевод всех других критериев в ограничения.
Рассмотрим основные показатели, используемые в качестве критериев оптимальности.
Максимум выпуска продукции в натуральных единицах: если на предприятии возможно соизмерение различных видов продукции через натуральные показатели штуки, тонны, метры, тонны условного топлива и др. (как правило, это предприятия химической отрасли, металлургии, топливной промышленности, пищевой отрасли), то целевая функция может принять следующий вид:
 (2.25)
(2.25)
Чаще всего в качестве критериального показателя используются различного рода стоимостные величины.
Максимум прибыли. При такой постановке задачи в качестве исходных параметров дана прибыль от реализации единицы продукции  .
.
Формализованная запись целевой функции представлена в виде уравнения 2.26
 (2.26)
(2.26)
Но возможна и другая запись целевой функции:
 (2.27)
(2.27)
где:
 оптовая цена одного изделия j-го вида;
оптовая цена одного изделия j-го вида;
 себестоимость изготовления одного изделия j-го вида.
себестоимость изготовления одного изделия j-го вида.
Максимум выпуска товарной продукции в стоимостном выражении:
 (2.28)
(2.28)
Максимум производительности труда:
 (2.29)
(2.29)
где:
S среднегодовая списочная численность промышленно-производственного персонала.
Более точно критерию максимума производительности труда соответствует целевая функция вида:
 (2.30)
(2.30)
где:
t годовой фонд времени одного рабочего,
dj трудоемкость изготовления одного изделия j-го вида,
r процент перевыполнения норм.
Система ограничений экономико-математической модели задачи определения производственного плана предприятия должна учитывать ограниченность производственных ресурсов и специфические условия работы предприятия, а также народно-хозяйственные потребности в его продукции. Основными видами ограничений являются:
· ограничения по затратам материалов, топлива, энергии и т.д.;
· ограничения по ресурсам основных фондов (прежде всего, технологического оборудования и производственных площадей), в частности, загрузка оборудования должна соответствовать его пропускной способности;
· ограничения по затратам труда с учетом профессионального состава работников;
· ограничения по финансовым активам;
· ограничения, характеризующие спрос на продукцию (объемные ограничения);
· критериальные ограничения (или ограничения по технико-экономическим показателям).
Ресурсные ограничения: расход ресурсов не должен превышать их установленных фондов, формализованная запись такого ограничения приведена в (2.9).
· Ограничения по оборудованию – отражают максимальное количество часов работы по группам оборудования и могут быть выражены в следующей форме:
 (
(  ) (2.31)
) (2.31)
где  - нормы затрат времени работы h-той группы оборудования по производству единицы j- того вида продукции,
- нормы затрат времени работы h-той группы оборудования по производству единицы j- того вида продукции,
 - эффективный фонд времени работы h-той группы оборудования,
- эффективный фонд времени работы h-той группы оборудования,
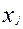 - объем производства j – той продукции (в натуральном выражении).
- объем производства j – той продукции (в натуральном выражении).
В случае, если задана производительность h - той группы оборудования по выпуску единицы j - той продукции (  ), то ограничение будет выглядеть следующим образом:
), то ограничение будет выглядеть следующим образом:
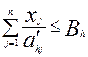 (
(  =
=  ) . (2.32)
) . (2.32)
Важность объемных ограничений определяется необходимостью учета при формировании производственной программы спроса на производимую предприятием продукцию.
Форма записи может быть: 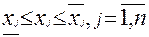 , (2.33)
, (2.33)
где  – нижний (верхний) пределы спроса на j-ый вид продукции.
– нижний (верхний) пределы спроса на j-ый вид продукции.
Если спрос задается по укрупненной номенклатуре, а промышленное предприятие определяет для себя объемные параметры выпуска по более детализированной номенклатуре, то ограничение по спросу принимает следующий вид:
 , (2.34)
, (2.34)
где  индекс группы изделий;
индекс группы изделий;
 количество групп изделий;
количество групп изделий;
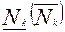 минимальное (максимальное) суммарное количество изделий в
минимальное (максимальное) суммарное количество изделий в  -ой группе;
-ой группе;
 индекс последнего изделия в группе
индекс последнего изделия в группе  .
.
И, наконец, ограничения по технико-экономическим показателям в моделях формирования производственной программы – это ограничения по показателям, которые задаются промышленным предприятием самостоятельно и определены в его планах. В качестве ограничений по технико-экономическим показателям выделяют следующие ограничения:
1) Ограничения по объему продаж:  (2.35)
(2.35)
где  - задаваемый нижний уровень объема продаж.
- задаваемый нижний уровень объема продаж.
2) Ограничение по прибыли:  (2.36)
(2.36)
где  – задаваемый нижний уровень прибыли.
– задаваемый нижний уровень прибыли.
3) Ограничение по себестоимости:  (2.37)
(2.37)
где  - себестоимость единицы j – той продукции,
- себестоимость единицы j – той продукции,
 – задаваемый верхний уровень себестоимости.
– задаваемый верхний уровень себестоимости.
4) Ограничения по капитальным вложениям:  (2.38)
(2.38)
 -цена единицы h-того вида оборудования,
-цена единицы h-того вида оборудования,
 - количество единиц приобретаемого h-того вида оборудования,
- количество единиц приобретаемого h-того вида оборудования,
 - общий объем капитальных вложений.
- общий объем капитальных вложений.
Приведенная система ограничений достаточно полная, дополнительные ограничения могут определяться в связи со спецификой предприятия.
Вопросы по теме
1. Виды представления оптимизационных моделей экономических задач.
2. В чем состоит преимущество экономико-математической модели перед другими моделями.
3. Как определяется устойчивость найденного оптимизационного плана к изменению объема ресурсов, к изменению коэффициентов целевой функции.
4. Возможные виды и представление критериев оптимальности.
5. Возможные виды и представление ограничений в оптимизационной модели.
2.2 Модели оптимизации использования производственной мощности предприятия.
Важнейшей задачей при формировании производственной программы является её обоснование размерами производственных мощностей. При этом производственная мощность предприятия характеризует его максимальные возможности по выпуску основной (профильной) продукции. В процессе экономико-математического моделирования величина производственной мощности определяется фондом времени работы ведущего оборудования.
Производственная программа и использование производственных мощностей тесно взаимосвязаны: с одной стороны, возможность увеличения выпуска продукции определяется мощностью установленного оборудования и степенью его использования; с другой стороны – коэффициенты использования производственных мощностей зависят от объема и ассортимента производимой продукции.
В целом задачи наилучшего использования производственных мощностей рассматриваются по двум вариантам – как задачи загрузки невзаимозаменяемых групп оборудования и задачи загрузки взаимозаменяемых групп оборудования.
При этом взаимозаменяемость различных групп оборудования рассматривается по отношению к выполнению технологических операций. Соответственно, под взаимозаменяемыми понимаются такие группы оборудования, путем использования которых возможно выполнение одинаковых деталеопераций, но с различной производительностью и, соответственно, затратами. Например, взаимозаменяемыми являются такие группы токарных станков, как станки – полуавтоматы, автоматы, станки полностью оснащенные универсальными инструментами и приспособлениями – потому что все они могут выполнять токарные операции, но с разной производительностью.
Оборудование нескольких качественно различных групп (токарных, шлифовальных, сварочных) невзаимозаменяемо в силу ряда причин: особенностей самой технологии обработки, ни один его вид не может заменить другой в случае, когда полезный фонд времени последнего исчерпан.
2.2.1 Модели оптимизации загрузки невзаимозаменяемого оборудования.
В задачах загрузки невзаимозаменяемого оборудования возможно использование различных критериев оптимизации, в том числе и рассмотренных ранее. В этом случае задача оптимизации загрузки оборудования сводится к подбору оптимальной производственной программы, позволяющей наилучшим образом использовать имеющиеся производственные мощности. Отличие модели оптимальной загрузки невзаимозаменяемого оборудования от более общей задачи оптимального использования ресурсов (2.8)÷(2.10) заключается в экономическом истолковании лимитов ресурсов  и норм затрат ресурсов
и норм затрат ресурсов  .
.
Введем для моделей загрузки оборудования следующие обозначения:
 индекс вида оборудовании,
индекс вида оборудовании,
 норма затрат станочного времени работы
норма затрат станочного времени работы  -ого оборудования на производство единицы
-ого оборудования на производство единицы  -ой продукции,
-ой продукции,
 полезный (эффективный фонд) времени оборудования вида
полезный (эффективный фонд) времени оборудования вида  .
.
Основной вид модели подбора программы под имеющиеся мощности может быть следующим:
 (2.39)
(2.39)


 (2.40)
(2.40)

 (2.41)
(2.41)
где  - прибыль от единицы j – той продукции,
- прибыль от единицы j – той продукции,
 - нормы затрат времени h- той группы оборудования на единицу j- той продукции,
- нормы затрат времени h- той группы оборудования на единицу j- той продукции,
 - эффективный фонд времени работы h- той группы оборудования.
- эффективный фонд времени работы h- той группы оборудования.
Требуется определить объем выпуска j - той продукции ( 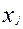 ) с целью получения максимального объема прибыли в пределах имеющихся мощностей. Здесь мы имеем частное проявление общей задачи на максимум результата при использовании ограниченного количества ресурсов.
) с целью получения максимального объема прибыли в пределах имеющихся мощностей. Здесь мы имеем частное проявление общей задачи на максимум результата при использовании ограниченного количества ресурсов.
В задаче загрузки оборудования может быть использован критерий максимума загрузки оборудования. Использование критерия на максимум загрузки может быть оправдано, ибо возможный выбор более станкоемкой продукции означает выбор более сложной в изготовлении (следовательно, и более дорогой, как правило, по цене или более прибыльной) продукции. Если нам неизвестны потребительские качества продукции, ее прибыль, себестоимость или мы можем ими пренебречь (например, значения этих показателей достаточно близки для разных видов продукции), то результатом производства может служить выпуск продукции вообще. Оптимизировать результаты производства в этом случае возможно, например, через затраты станочного времени. В этом случае целевая функция может быть представлена так:
 (2.42)
(2.42)
Как правило, для одной и той же экономической задачи может быть представлено несколько моделей. В частности задача максимума загрузки оборудования может быть поставлена иначе. Вспомним, что для решения задачи методом линейного программирования система ограничений (неравенства) представляются в виде уравнений добавлением в левую часть неравенств новых переменных дополнительных неизвестных  , экономический смысл которых в нашей задаче неиспользованный остаток фонда времени работы
, экономический смысл которых в нашей задаче неиспользованный остаток фонда времени работы  -ого оборудования. Так как все дополнительные неизвестные так же будут измеряться в станко-часах, то их сумма означает совокупный неиспользуемый остаток фонда времени работы оборудования всех видов. В этом случае модель на максимум загрузки оборудования можно записать следующим образом:
-ого оборудования. Так как все дополнительные неизвестные так же будут измеряться в станко-часах, то их сумма означает совокупный неиспользуемый остаток фонда времени работы оборудования всех видов. В этом случае модель на максимум загрузки оборудования можно записать следующим образом:
 (2.43)
(2.43)

 (2.44)
(2.44)
 (2.45)
(2.45)
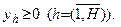 (2.46)
(2.46)
 Если заданы плановые задания по выпуску продукции вида
Если заданы плановые задания по выпуску продукции вида
 , (2.47)
, (2.47)
то можно решить задачу по отысканию значений сверхпланового выпуска продукции  , максимизирующих загрузку свободных остатков станочного времени. Обозначим свободные остатки фондов работы оборудования после обязательного выполнения плана
, максимизирующих загрузку свободных остатков станочного времени. Обозначим свободные остатки фондов работы оборудования после обязательного выполнения плана
 (2.48)
(2.48)
Модель задачи поиска сверхплановой продукции по критерию максимума загрузки оборудования примет вид
 (2.53)
(2.53)

 (2.54)
(2.54)
 (2.55)
(2.55)
 (2.56)
(2.56)
После решения задачи значения исходных переменных  могут быть получены простым суммированием:
могут быть получены простым суммированием:  .
.
Введение в модель ограничений по производственной программе, как и в задаче на максимум прибыли, целесообразно лишь при существовании нескольких способов производства одноименной продукции. Тогда оптимизация становится возможной за счет выбора наилучших способов производства каждой продукции в рамках заданных фиксированных планов их выпуска:
 (2.53)
(2.53)

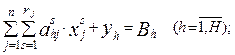 (2.54)
(2.54)
 (2.55)
(2.55)
 (2.56)
(2.56)
 (2.57)
(2.57)
2.2.2 Модели загрузки взаимозаменяемых групп оборудования.
Модели загрузки взаимозаменяемых групп оборудования в процессе оптимизации использования производственных мощностей применяются при решения задачи оптимального распределения работ по группам взаимозаменяемого оборудования для выполнения заданной производственной программы по тому или иному критерию оптимальности.
Разработку модели загрузки взаимозаменяемого оборудования рассмотрим на следующем примере.
Пример 2.1. Найти оптимальный план распределения шести заказов между четырьмя взаимозаменяемыми станками с целью достижения максимума прибыли.
Исходные данные задачи представлены в таблице 2.2.
Таблица 2.2
| № заказа | Кол. Изделий (план) | Производительность по станкам (шт/час) | Себестоимость (тыс.руб/шт) | Цена (тыс.руб/шт.) | ||||||
| I | II | III | IV | I | II | III | IV | |||
| А | 2,5 | 2,0 | 4,0 | 3,0 | 5,1 | |||||
| Б | 1,2 | 1,0 | 1,7 | 1,5 | 2,0 | |||||
| В | 0,65 | 0,6 | 0,7 | 1,8 | 1,5 | |||||
| Г | - | 4,0 | 3,0 | 3,5 | - | 6,8 | ||||
| Д | 3,0 | 2,5 | 3,2 | 3,4 | 4,0 | |||||
| Е | - | - | - | - | 1,8 | - | - | 3,0 | ||
Полезный фонд времени работы станков составляет соответственно по станкам (в часах): 40,40, 80, 60.
Введем обозначения:
 - объем выпуска
- объем выпуска  -ой продукции на
-ой продукции на  -ой разновидности оборудования,
-ой разновидности оборудования,
Chj- затраты в стоимостном выражении на производство  - ой продукции на
- ой продукции на  - той разновидности оборудования,
- той разновидности оборудования,
 ─ цена единицы
─ цена единицы  - той продукции.
- той продукции.
Экономико-математическая модель задачи распределения выполнения работ по станкам, обеспечив при этом максимум прибыли:
 (2.58)
(2.58)

 (
( 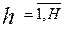 ) (2.59)
) (2.59)
 (
(  ) (2.60)
) (2.60)
 . (2.61)
. (2.61)
Указанные задачи могут быть решены и на другие критерии оптимальности.
Отметим, что характерной особенностью задач оптимального распределения работ по группам взаимозаменяемого оборудования для выполнения заданной производственной программы является наличие ограничения по выпуску продукции. Указанное ограничение в задачах формирования оптимальной производственной программы, т.е. в моделях загрузки невзаимозаменяемого оборудования, может быть задано, однако не является обязательным.
Вопросы по теме
1. Понятие взаимозаменяемого и невзаимозаменяемого оборудования.
2. Как соотносятся модели загрузки невзаимозаменяемого оборудования и общая модель оптимизации производственной программы при ограниченных ресурсах.
3. В каких моделях загрузки оборудования обязательно наличие ограничения по выпуску продукции.
4. В модели (2.56)÷(2.59) чем является величина  (экономический смысл).
(экономический смысл).
5. В каких моделях может быть поставлена целевая функция на максимум загрузки оборудования.
6. Пусть в задаче п. 2.1.1 дополнительно в качестве исходных данных задан суточный план выпуска по видам продукции. Как изменится экономико-математическая модель задачи.
7. К задаче п. 2.2.1 составить модель максимизации сверхпланового выпуска продукции (по стоимости).
2.3 Оптимизационные модели экономии материальных ресурсов предприятия
Важнейшей частью производственного процесса на предприятии является технологическая подготовка производства (ТПП). Содержание ТПП определяется отраслевыми особенностями предприятия. На предприятиях машиностроения в подготовительных цехах, участках осуществляется подготовка заготовок из исходного материала – нарезкой, штамповкой и др., в прядильном производстве ТПП заключается в смешивании волокон для дальнейшего изготовления пряжи, в сталелитейных предприятиях ТПП это составление шихты как смеси шихтовых материалов. Во всех этих случаях стоит задача оптимизации ТПП с целью экономии материальных ресурсов при получении заданного вида заготовок или смеси с заранее определенными свойствами при минимальных затратах. К этому же типу задач мы отнесли транспортную задачу, при решении которой оптимизируется доставка груза от многочисленных поставщиков многочисленным потребителям с целью минимизации суммарных затрат на перевозки.
Дата добавления: 2014-11-13; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |