
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
TERMINATE 4 страница. 2.3.1 Модели оптимизации состава промышленных смесей.
2.3.1 Модели оптимизации состава промышленных смесей.
В ряде производств (металлургической, пищевой, нефтеперерабатывающей отраслях промышленности) готовая продукция получается путем смешивания различных исходных компонентов (сырья), при этом качество готовой продукции должно соответствовать определенным требованиям при достижении максимального экономического эффекта.
Проблема рационального использования сырья в этих случаях может быть решена путем применения экономико-математических моделей оптимального составления смесей.
Как правило, исходные компоненты смеси взаимозаменяемы по содержанию качественных характеристик. При этом важно обеспечить соответствие готовой продукции по указанным качественным характеристикам необходимым требованиям, которые определяются стандартами и сертификатами.
Модель задачи позволяет найти такой набор компонентов смесей и их количественное соотношение, которое удовлетворяет заданным технологическим требованиям по качеству, а также требованиям принятого критерия (минимальной себестоимости или максимальной прибыли).
Задача смешивания может быть рассмотрена в натуральных единицах или в долях.
Рассмотрим задачу определения количества сырья, необходимого для получения смеси заданного объема.
На предприятии изготавливается бензин А-76, в котором содержание серы не более 0,3%, а октановое число должно быть не ниже 76.
Данные об используемых компонентах (видах сырья ─ нефтепродуктах) приведены в таблице 2.3. Требуется определить, сколько тонн каждого компонента нужно взять для получения 1000 т бензина А-76, чтобы при этом себестоимость бензина была минимальной.
Таблица 2.3
| Показатель | Компоненты автомобильного бензина (нефтепродукты) | |||
| Октановое число | ||||
| Содержание серы, % | 0,35 | 0,35 | 0,3 | 0,2 |
| Ресурсы, т | ||||
| Себестоимость (ден.ед.) |
Пусть  ─ оптимальные количества соответствующих компонентов, входящих в состав готовой смеси.
─ оптимальные количества соответствующих компонентов, входящих в состав готовой смеси.
Математическая модель задачи представлена в (2.62)÷(2.67):
целевая функция:
 (2.62)
(2.62)
ограничение по октановому числу:
 ; (2.63)
; (2.63)
ограничение по содержанию серы:
 ; (2.64)
; (2.64)
ограничение по объему готовой продукции:
 ; (2.65)
; (2.65)
ограничение по имеющимся ресурсам:
 (2.66)
(2.66)
условие неотрицательности переменных:
 (2.67)
(2.67)
В общем виде задача формализуется следующим образом:

 – индекс качественной характеристики; имеет отношение к исходным видам сырья, материалов и к готовой продукции (
– индекс качественной характеристики; имеет отношение к исходным видам сырья, материалов и к готовой продукции (  );
);
 - индекс исходных компонентов смеси (
- индекс исходных компонентов смеси (  );
);
 ─ имеющийся объем
─ имеющийся объем  -ой компоненты (сырья);
-ой компоненты (сырья);
 - содержание
- содержание  -той качественной характеристики в единице
-той качественной характеристики в единице  -го исходного компонента;
-го исходного компонента;
 - содержание
- содержание  -той качественной характеристики в единице готовой смеси; для
-той качественной характеристики в единице готовой смеси; для  качественных характеристик, ухудшающих качество продукции, задается верхняя граница содержания той или иной качественной характеристики, а для
качественных характеристик, ухудшающих качество продукции, задается верхняя граница содержания той или иной качественной характеристики, а для  качественных характеристик, улучшающих качество продукции, задается нижняя граница содержания той или иной качественной характеристики;
качественных характеристик, улучшающих качество продукции, задается нижняя граница содержания той или иной качественной характеристики;
 ─ имеющийся ресурс
─ имеющийся ресурс  -ой компоненты;
-ой компоненты;
 - цена единицы
- цена единицы  - ой исходной компоненты (включая расходы на переработку);
- ой исходной компоненты (включая расходы на переработку);
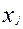 - количество
- количество  - ой исходной компоненты, которое входит в готовую смесь.
- ой исходной компоненты, которое входит в готовую смесь.
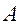 ─ общее количество готовой продукции, которое следует изготовить по плану.
─ общее количество готовой продукции, которое следует изготовить по плану.
Формализованная модель задачи оптимизации состава требуемого объема смеси представлена в (2.68) ÷ (2.72)
Целевая функция:
 (2.68)
(2.68)
ограничения, ухудшающие качества:
 (2.69)
(2.69)
ограничения, улучшающие качества:
 (2.70)
(2.70)
ограничение по плану производства продукции:
 (2.71)
(2.71)
ограничение по ресурсам:
 (2.72)
(2.72)
Вторая разновидность смесевых задач касается оптимизации структуры готовой продукции, безотносительно к объемам. Рассмотрим пример такой задачи.
Пример 2.2. Пусть требуется изготовить некоторую единицу объема сплава, содержащего не менее 4% никеля, не более 75% железа и 20% прочих веществ. Известна стоимость различных видов сырья и процентное содержание в них соответствующих элементов (табл. 2.4)
Таблица 2.4
| Вещество | Содержание элементов для каждого вида сырья, % | ||
| Железо | |||
| Никель | |||
| Прочие | |||
| Стоимость единицы сырья (ден.ед.) |
Определить оптимальную структуру сплава, при которой стоимость единицы сплава будет минимальной.
Математическая модель задачи:
 (2.73)
(2.73)

 ; (2.74)
; (2.74)
 ; (2.75)
; (2.75)
 (2.76)
(2.76)
 ; (2.77)
; (2.77)
 (2.78)
(2.78)
Экономико-математическая модель этой задачи будет включать выражения:
целевая функция:
 (2.79)
(2.79)
ограничения на качество смеси:
 (2.80)
(2.80)
 (2.81)
(2.81)
ограничение по формированию структуры смеси:
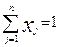 . (2.82)
. (2.82)
неотрицательность переменных:
 . (2.83)
. (2.83)
В данной задаче минимизируется стоимость единицы (кг, т и т.д.) смеси. Очевидно, что при любых объемах переработки сырья и выпуска готовой продукции, оптимальному плану будет соответствовать одна и та же структура смеси, т.е. соотношение в ней отдельных составных частей видов сырья.
Модели общего вида применяются при решении “задач о диете” – а именно задач составления оптимальных кормовых рационов, задач составления смесей минеральных удобрений, задач составления смесей нескольких химических веществ.
Более сложные модели задач смешивания составляются в тех случаях, когда в результате смешивания одних и тех же исходных компонентов могут быть получены различные виды готовой продукции. Тогда наряду с ограничениями по исходным компонентам задаются объемные ограничения по выпуску готовой продукции. Типичным примером таких моделей является модель смешивания нефтепродуктов. Рассмотрим пример постановки задачи смешивания нефтепродуктов.
Для получения готовых бензинов на установку поступают различные исходные компоненты (нефтепродукты). Оптимальный план позволяет определить, в каких количествах должны смешиваться различные исходные компоненты, чтобы различные сорта бензина (готовой продукции) выпускались в соответствии с планом и заданными по стандарту качественными характеристиками при обеспечении рентабельной работы установки.
Введем обозначения:
 - индекс качественной характеристики, применяется по отношению к исходным нефтепродуктам и к сортам бензина;
- индекс качественной характеристики, применяется по отношению к исходным нефтепродуктам и к сортам бензина;
 - индекс исходного нефтепродукта;
- индекс исходного нефтепродукта;
k –индекс вида готового бензина,  ;
;
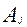 - ограниченное количество j-го вида исходного нефтепродукта;
- ограниченное количество j-го вида исходного нефтепродукта;
Bk – плановое задание по выпуску бензина k-го сорта,
hij – содержание i – той качественной характеристики в единице j – го исходного нефтепродукта;
Hik – содержание i - той качественной характеристики в бензине k- го вида;
Cj – цена исходного j- го нефтепродукта;
 – цена бензина k - го вида.
– цена бензина k - го вида.
Требуется определить Xjk – количество j–го вида исходного нефтепродукта, направляемое на получение k- го вида бензина.
Модель задачи представлена в выражениях (2.84)÷(2.88):

 (2.84)
(2.84)
по объему ресурсов:  (
(  ), (2.85)
), (2.85)
по выпуску продукции: 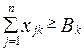 (
(  ), (2.86)
), (2.86)
по качественным характеристикам:
 (
(  ;
;  ) (2.87)
) (2.87)
 (
(  ;
;  ). (2.88)
). (2.88)
Все сформулированные смесевые задачи решаются методами линейного программирования.
2.3.2 Модели оптимизации раскроя промышленных материалов
В промышленном производстве в процессе подготовки производства часто различные исходные материалы подвергаются разрезке на заготовки меньших размеров. Материалы могут быть в виде прутков, труб, листов. Раскрой материалов (из металла, картона, бумаги, фанеры, древесины и т.п.) может производиться где угодно: в заготовительных участках цехов предприятий, мастерских и других производствах. В процессе раскроя неизбежны отходы из-за некратности размеров заготовки размерам исходного материала; по этой причине имеются значительные потери материалов в виде отходов.
Свести отходы к минимуму позволяет применение принципов линейного программирования в виде планирования "совместных раскроев".
Совместный раскрой предполагает, что заранее разрабатывается ряд возможных вариантов разрезки материала определенного размера на произвольные комбинации различных заготовок. Каждый такой вариант характеризуется различным составом заготовок, выкраиваемых из единицы материала, и разной величиной отходов. В этих вариантах не учтено условие комплектности. Для удовлетворения требования комплектности уровни возможного использования этих вариантов принимаются за переменные, а затем методами линейного программирования решается задача с учетом условия комплектности заготовок. Рассмотрим типовую задачу на оптимизацию раскроя.
Пример 2.3.Снабженческо-сбытовая фирма получает от поставщиков прутки стального проката длиной 600см. Согласно заявкам потребителей, требуются заготовки трех видов в следующих количествах: 150 тыс.шт. длиной 250см., 140 тыс.шт. длиной 190см. и 48 тыс.шт. длиной 100см. Сформулируем модель задачи оптимального раскроя с минимумом отходов. Наиболее трудоемкий этап в процессе построения модели рассматриваемой задачи заключается в определении всех возможных вариантов раскроя. В таблице 2.5 перечислены варианты раскроя одного прутка и размер отхода, полученного при раскрое одного прутка по каждому варианту (в см):
Таблица 2.5
| Номер варианта раскроя (j) | Количество заготовок (aij) | Остаток (сj) | ||
| L4=250см. | L2 =190 см. | L3= 100 см. | ||
| - | - | |||
| - | ||||
| - | - | |||
| - | ||||
| - | ||||
| - | - | - |
Пусть x1, x2, x3, x4, x5, x6, x7 количество прутков, раскраиваемых по каждому варианту. Ниже приведена математическая модель задачи в виде выражений (2.89)÷(2.93):
целевая функция на минимум отходов:
 , (2.89)
, (2.89)
ограничения по условиям комплектности

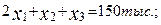 (2.90)
(2.90)
 (2.91)
(2.91)
 (2.92)
(2.92)
условие неотрицательности
хi ³ 0;  (2.93)
(2.93)
Для построения экономико-математической модели задачи примем следующие обозначения:
i – индекс вида заготовки (  );
);
j – индекс варианта раскроя (  );
);
Ai- требуемое количество заготовок i – го вида, необходимое для комплектности;
aij – количество заготовок i-го вида при раскрое единицы исходного материала по j-му варианту;
cj –длина отхода при раскрое по j-му варианту.
Требуется определить xj – количество прутков, раскраиваемых по j-му варианту. Формализованный вид экономико-математической модели представлен выражениями (2.94)÷(2.97):
целевая функция по критерию минимум отходов имеет вид:
 , (2.94)
, (2.94)
а по критерию минимума раскраиваемых единиц исходного материала
 (2.95)
(2.95)
при условиях:

 (
(  ); (2.96)
); (2.96)
 . (2.97)
. (2.97)
Получилась обычная задача линейного программирования, которую можно дополнить требованием целочисленности величины xj . Во многих случаях, решения задач с обеими указанными целевыми функциями совпадают.
При определении возможных вариантов раскроя необходимо учитывать ряд условий: пусть L ─ длина раскраиваемого материала, а li ─ длина заготовки i-го вида, тогда признак полноценности варианта раскроя представлен соотношением (2.98):
 (2.98)
(2.98)
а длина отхода для любого варианта раскроя должна быть меньше длины самой короткой заготовки:
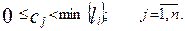 (2.99)
(2.99)
Рассмотренная задача предусматривает раскрой длинномерных материалов (прутков, труб, профильного проката и др.). На практике приходится вести раскрой как рулонного, так и листового материала.
Для экономико-математической модели задачи раскроя рулонного материала изменится экономический смысл ряда обозначений:
aij ─ количество полос i-го размера, раскраиваемых из рулона по j-му
варианту раскроя;
cj ─ размер краевого отхода при раскрое рулона по j-му варианту;
Ai ─ общее количество полос i-го размера, которое нужно получить при раскрое.
Решения задач оптимизации промышленных смесей и раскроя, представленных моделями (2.68÷ 2.72), (2.79÷2.83) и (2.94÷ 2.97) производится по программе алгоритма симплексного метода.
Вопросы по теме
1. Виды моделей оптимизации состава промышленных смесей.
2. Понятие плана совместного раскроя.
3. Как удовлетворяется требование комплектности раскраиваемых материалов.
4. Приведите выражения, отражающие условия.
5. Составьте модель задачи раскроя листового материала.
2.3.3 Транспортная задача
Одной из часто решаемых задач хозяйственного управления является задача по разработке рационального плана транспортных перевозок. Основная цель оптимизации организации перевозок минимизация затрат на их выполнение. В экономико-математическом моделировании эта задача получила название транспортной задачи (или задачей оптимизации прикрепления потребителей к поставщикам). Транспортные задачи нашли широкое применение при решении оптимизационных моделей регионального и межотраслевого регулирования, оптимизации размеров и размещения производств, которые рассматриваются в Разделе 4.2.
2.3.3.1 Общая постановка транспортной задачи.
В общем виде формулировка транспортной задачи осуществляется следующим образом: требуется перевезти определенное количество однородного груза из  пунктов отправления в
пунктов отправления в 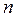 пунктов назначения. Известны расходы на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения.
пунктов назначения. Известны расходы на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения.
Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь груз от поставщиков вывозится, каждый потребитель получает требуемое количество груза, и вместе с тем, общая величина транспортных издержек минимальна.
Для составления экономико-математической модели задачи введем обозначения:
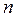 число пунктов отправления;
число пунктов отправления;
 число пунктов назначения;
число пунктов назначения;
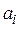 общее количество груза в i-м пункте отправления;
общее количество груза в i-м пункте отправления;
 общее количество груза, необходимое в j-м пункте назначения;
общее количество груза, необходимое в j-м пункте назначения;
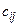 затраты на транспортировку единицы груза из i-го пункта
затраты на транспортировку единицы груза из i-го пункта
отправления в j-й пункт назначения;
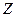 совокупные затраты на перевозку всего груза;
совокупные затраты на перевозку всего груза;
 исходно неизвестное количество груза, которое перевозится из
исходно неизвестное количество груза, которое перевозится из
i-го пункта отправления в j-й пункт назначения.
Экономико-математическая модель задачи представлена формулами (2.100)÷(2.103):
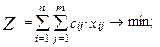 (2.100)
(2.100)

 (2.101)
(2.101)
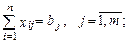 (2.102)
(2.102)
 (2.103)
(2.103)
Целевая функция (2.100) минимизирует совокупные затраты на транспортировку всех партий грузов из всех пунктов отправления во все пункты назначения. Система ограничений (2.101) говорит о том, что весь груз из каждого пункта его сосредоточения должен быть вывезен. Система ограничений (2.102) говорит о том, что потребность в грузе в каждом пункте назначения должна быть удовлетворена. Система ограничений (2.103) говорит о том, что по любому маршруту некоторое количество груза либо перевозится, либо нет.
Транспортная задача является задачей линейного программирования с (n + m) ограничениями уравнениями и (n x m) неизвестными.
Транспортная задача, у которой суммарное наличие груза совпадает с суммарной потребностью, т.е. выполняется равенство (2.104)
 (2.104)
(2.104)
называется закрытой (сбалансированной) транспортной задачей. Если условие (2.104) выполняется, то доказано, что транспортная задача имеет оптимальное допустимое решение. В случае если условие (2.104) не выполняется, то транспортная задача называется открытой. Решение транспортных задач с открытой моделью сводится к решению задач с закрытой моделью путем добавления фиктивного поставщика или фиктивного потребителя так, чтобы выполнялось условие (2.104). Транспортная задача относится к задачам распределительного типа и решается симплексным методом. Приведем прием решения транспортной задачи с помощью средства «Поиск решения» EXCEL.
Пример 2.4. Условия транспортной задачи представлены в таблице 2.6.
Таблица 2.6
| Поставщики | Мощности поставщиков (ai) | Мощности потребителей (bj) | |||
В примере однородный груз должен быть доставлен от четырех поставщиков (n=4) четырем потребителям (m=4). Мощности поставщиков (  ) и потребность в этом грузе в каждом пункте назначения (
) и потребность в этом грузе в каждом пункте назначения (  ) приведены в таблице 2.6. В левых нижних углах каждой клетки рабочей таблицы, которые соответствуют всем возможным путям перевозки груза из всех пунктов отправления во все пункты назначения, указаны затраты на транспортировку единицы груза по данному маршруту (
) приведены в таблице 2.6. В левых нижних углах каждой клетки рабочей таблицы, которые соответствуют всем возможным путям перевозки груза из всех пунктов отправления во все пункты назначения, указаны затраты на транспортировку единицы груза по данному маршруту (  ). Суммарные запасы груза (550) и потребности в грузе (550) совпадают, значит это закрытая транспортная задача. Требуется составить план перевозок, обеспечивающий минимальные затраты на транспортировку всего груза.
). Суммарные запасы груза (550) и потребности в грузе (550) совпадают, значит это закрытая транспортная задача. Требуется составить план перевозок, обеспечивающий минимальные затраты на транспортировку всего груза.
2.3.3.2 Подготовка к решению транспортной задачи в EXCEL.
Для решения задачи средством EXCEL «Поиск решения» необходимо разместить в рабочем листе исходные данные и подготовить поля для размещения условий и результатов решения задачи (выбор ячеек листа произвольный). Таким образом будет создана «Электронная модель транспортной задачи».
На рис. 2.2 приведен пример подготовки данных на рабочем листе EXCEL для решения этой задачи.

Рис. 2.2 Пример подготовки размещения данных транспортной задачи для решения в EXCEL.
Рекомендуется следующий порядок работы в рабочем листе.
1) Выделить диапазон ячеек:
− для размещения исходной матрицы (A14:E19);
− для размещения матрицы оптимальных перевозок (матрица для размещения результатов после решения задачи) (A4:F9), рекомендуется для наглядности в обе матрицы внести текст пояснений;
2) матрицу исходных данных (A14:E19) заполнить исходными данными таблицы 2.6 (значения ai, bj, cij).
В матрице результата во все ячейки диапазона (B6:E9) внести «1» в качестве исходных значений объемов поставок xij, после решения задачи в этих ячейках будут находиться значения поставок, обеспечивающие минимальные затраты на перевозку груза.
3) ввести в ячейки (В10:Е10) итог поставок по потребителям: в ячейку В10 ввести формулу =СУММ(В6:В9) − итог поставок по 1-му потребителю, скопировать эту формулу в ячейки (С10:Е10);
4) ввести в ячейки (F6:F9) итоги реализации мощности каждого из поставщиков: в ячейку F6 ввести формулу =СУММ(В6:Е6) − итог реализации поставок от 1-го поставщика, скопировать эту формулу в ячейки (F7:F9);
5) выделить ячейку для ввода формулы целевой функции, например В21и ввести формулу =СУММПРОИЗВ(В16:Е19;В6:Е9) −суммарнаястоимость перевозок по всем направлениям.
6) в рабочем окне режима «Поиск решения» указать в качестве ячейки целевой функции В21, при вводе ограниченийделать ссылку на отведенные диапазоны (см. данные таблицы 2.7):
Таблица 2.7
| Левая часть ограничения | Знак | Правая часть ограничения | Экономический смысл |
| (В10:Е10) | = | (В15:Е15) | Спрос потребителей должен быть удовлетворен |
| (F6:F9) | = | (А16:А19) | Весь груз от поставщиков должен быть вывезен |
Дата добавления: 2014-11-13; просмотров: 690; Мы поможем в написании вашей работы!; Нарушение авторских прав |