
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Деформации растяжения и сжатия.
Определим изменение длины бруса.

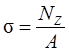
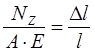
Изменение длины бруса равно алгебраической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле Гука: абсолютное удлинение прямо пропорционально продольной силе, длине и обратно пропорционально жёсткости сечения бруса

где Ni, li, Аi – соответственно продольная сила, длина и площадь сечения в пределах каждого участка бруса;
Произведение АЕ – условно называется жёсткостью сечения бруса при растяжении и сжатии.
22. Изобразите и объясните диаграмму растяжения низкоуглеродистой стали и ее характерные параметры.
При испытании на растяжение нагрузка к образцам прикладывается статически, т.е. медленно, плавно, с постепенным непрерывным нарастанием.
Для того, чтобы результаты испытаний, проведённых различными лабораториями, были сопоставимы, используются стандартные типы и размеры образцов.
Образец закрепляют концами в захваты разрывной машины. Затем растягивают плавно возрастающей нагрузкой. В процессе испытания самопишущее автоматическое устройство машины вычерчивает диаграмму растяжения, на которой по оси ординат отмечается величина нагрузки, а по оси абсцисс – величина абсолютных удлинений. Эта диаграмма зависит не только от свойств материала, но и от размеров испытуемого образца. Чтобы получить диаграмму, характеризующую только механические свойства материала, перестраивают диаграмму в координатах σ – ε . Эти две диаграммы отличаются друг от друга лишь масштабами.


где А0 и l0 – первоначальная площадь поперечного сечения образца и первоначальная длина.
На рисунке представлена диаграмма растяжения низкоуглеродистой стали.

В начальный момент σ0=0, ε0 =0. При увеличении нагрузки стержень получает удлинение, которое растёт пропорционально силе. Прямая ОА графически выражает закон Гука. В образце возникают упругие деформации.
Диаграмма имеет следующие характерные точки.
Точка А соответствует пределу пропорциональности.
Предел пропорциональности (σpr) ─ это наибольшее напряжение, до которого деформации растут пропорционально нагрузке, т.е. справедлив закон Гука.
Тангенс угла наклона α прямого участка ОА к оси абсцисс равен модулю упругости Е.
Выше точки А диаграмма представляет собой кривую линию, деформации растут быстрее роста напряжений. В образце наряду с упругими возникают и небольшие остаточные деформации, которые настолько малы (меньше 0,05%), что ими пренебрегают. Точка А практически соответствует и пределу упругости.
Предел упругости(σel) ─ это наибольшее напряжение, до которого в образце не возникают остаточные деформации.
Начиная с точки С диаграмма имеет горизонтальный участок, показывающий, что деформации растут даже без увеличения нагрузки – площадка текучести. Точка С соответствует пределу текучести.
Предел текучести(σу) ─ это напряжение, при котором происходит рост пластических деформаций при практически постоянной нагрузке.
При достижении предела текучести повышается температура образца; поверхность его становится матовой, так как на ней появляется сетка линий Людерса-Чернова, наклонённых под углом 450 к оси стержня. Эти линии представляют собой следы максимальных сдвигов частиц материала, соответствующие наибольшим касательным напряжениям τmax. В результате этих сдвигов образец получает пластические деформации.


Предел прочности(σu) ─ это условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом до разрушения.
Пластичность материала характеризуются относительным остаточным удлинением:
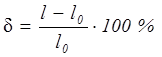
Относительное остаточное поперечное сужение:

Дата добавления: 2015-02-10; просмотров: 550; Мы поможем в написании вашей работы!; Нарушение авторских прав |