Контрольная работа № 1. Типичные задачи

1. Найти и изобразить в декартовой системе координат области выпуклости и вогнутости функции . Выпуклы ли построенные области?

2. Задачу нелинейного программирования при привести к стандартному виду. Изобразить допустимое множество и линии уровня целевой функции; решить задачу графически. Проверить, выполняются ли условия теоремы Вейерштрасса о существовании решения. На рисунке проверить выполнение условий Куна – Таккера в угловых точках допустимого множества (т. е. в точках, в которых число активных ограничений не меньше числа переменных) и в точках касания линии уровня целевой функции с границами допустимой области. Найти точки, в которых условия Куна – Таккера выполняются, и определить, какие из ограничений являются активными в таких точках. Выписать условия Куна – Таккера в найденных точках и рассчитать значения двойственных переменных. Сделать обоснованный вывод о наличии или отсутствии локального (глобального) максимума во всех рассмотренных точках.

3. Фабрика по производству мороженого может выпускать пять сортов мороженого. При производстве мороженого используется два вида сырья (молоко и наполнители), запасы которых известны. Известны и удельные затраты сырья, а также цены продукции. Требуется построить план производства, который обеспечивает максимум дохода.

4. Подготовлено несколько вариантов стратегий 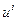управления фирмой. По каждой стратегии оценен объем прибыли для различных прогнозов 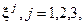будущей ситуации, причем не известно, какой из прогнозов реализуется. Вероятность реализации прогноза также не известна. Величины прибыли при реализации каждого из прогнозов приведены в таблице. Найти наилучшие стратегии по критериям максимакса, Байеса – Лапласа, Гурвича, Сэвиджа, а также наилучшую гарантирующую стратегию и максимальную гарантированную оценку прибыли.

5. Рассмотреть задачу целевого программирования, в которой множество допустимых решений задается неравенствами и 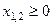, критерии заданы соотношениями 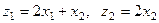, а целевая точка совпадает с идеальной точкой z*, отклонение от которой задается функцией . Найти и изобразить множество достижимых критериальных векторов Z, его паретову границу P(Z) и идеальную точку z*. Изобразить линии уровня функции . Графически решить задачу нахождения достижимой точки (z’₁, z’₂), дающей минимум отклонения от идеальной точки; аналитически записать задачу минимизации отклонения от идеальной точки в виде задачи линейного программирования.

Формируемые компетенции: ПК-1, 2, 4, 5, 14.