Теоретическое введение. Если прямой упругий стержень обоими концами свободно положить на твердые опоры и нагрузить в середине грузом весом

Если прямой упругий стержень обоими концами свободно положить на твердые опоры и нагрузить в середине грузом весом , то середина стержня опустится, т. е. стержень согнется. При таком изгибе верхние слои стержня будут сжиматься, нижние - растягиваться, а некоторый средний слой, который называют нейтральным слоем, сохранит длину и только претерпит искривление.

Перемещение , которое получает середина стержня, называется стрелой прогиба. Стрела прогиба тем больше, чем больше нагрузка, и, кроме того, она зависит от формы и размеров стержня и от его модуля упругости.

Для деформаций растяжения и сжатия модуль упругости называется модулем Юнга и численно равен напряжению (т. е. упругой силе, приходящейся на единицу площади поперечного сечения тела), возникающему в образце при увеличении (уменьшении) его длины в два раза.

Найдем связь между стрелой прогиба и характеристиками упругого стержня. В данной работе используется пластина прямоугольного сечения размерами L (длина), h (высота), b (ширина).

Под воздействием внешней силы пластина искривляется, и ее форма может быть описана функцией (см. рис. 1). Возникающие в пластине силы упругости пропорциональны кривизне пластины, т. е. второй производной . Условие равновесия имеет вид:

[1]

где - модуль Юнга; - коэффициент (геометрический момент инерции прямоугольного сечения пластины, относительно осевой линии), определяемый геометрией пластины; - изгибающий момент сил.

Таким образом, получаем дифференциальное уравнение для формы пластины: 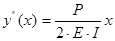, интегрируя которое, находим: .

Константу интегрирования определим из условия равенства нулю наклона пластины в ее центре: , откуда . После второго интегрирования имеем:

[2]

Стрела прогиба по модулю равна смещению середины пластины:

[3]

Подставляя в [3]: , где 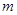- масса груза, - ускорение свободного падения, окончательно находим:

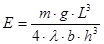[4]

Интервал надежности.

Интервал надежности можно оценить по правилам расчета погрешности косвенного измерения:

[5]

где - коэффициент Стьюдента, зависящий от доверительной вероятности p и числа измерений n.

Записываем результат в виде: ; p = ;