Теоретическое введение. Часть механики, занимающаяся изучением движения жидкости, называется гидродинамикой

Часть механики, занимающаяся изучением движения жидкости, называется гидродинамикой. Основные законы гидродинамики (теорема о неразрывности струи, уравнение Бернулли и .д.) получены для так называемой «идеальной жидкости», которая должна быть абсолютно несжимаемой. Идеальная жидкость служит лишь более или менее хорошим приближением к реальным жидкостям.

Всякая реальная жидкость обладает вязкостью или внутренним трением, т.е. свойство оказывать сопротивление перемещению одних слоев жидкости относительно других. Со стороны слоя, движущегося более быстро, на слой, движущейся медленнее, действует ускоряющая сила и, наоборот, со стороны медленного слоя на более быстрый действует задерживающая сила. Эти силы направлены по касательной к поверхности слоев.

Пусть два слоя жидкости (рис. 1), отстоящие друг от друга на расстоянии , имеют соответственно скорости, и . Положим . Направление, в котором отсчитывается , перпендикулярно к скорости течения слоёв.

Предел отношения 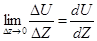показывает, как быстро меняется скорость течения жидкости при переходе от слоя к слою и называется градиентом скорости.

Сила внутреннего трения, действующая между двумя слоями с поверхностью соприкосновения слоёв S, пропорциональна градиенту скорости, площади рассматриваемой поверхности и определяется законом Ньютона для жидкостей и газов.

[1]

где 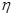- коэффициент вязкости жидкости, измеряется в .

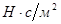Коэффициентом вязкости жидкости называется сила внутреннего трения, возникающая на единице площади поверхности соприкасающихся слоёв, движущихся с градиентом скорости, равным единице и весьма сильно зависит от температуры.

Описание установки и расчетные формулы.

Установка представляет собой вертикально установленный стеклянный цилиндр, заполненный до краев, вязкой жидкостью – глицерином. На боковой поверхности цилиндра, расположены две метки, на расстоянии 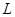друг от друга (рис. 2).

Для нахождения коэффициента вязкости используется метод Стокса, основанный на измерении времени падения в жидкости твёрдого шарика малых размеров.

На шарик, диаметром 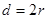и плотностью , падающий в вязкой жидкости, плотностью , действуют три силы:

1. Cила тяжести:

; [2]

2. Выталкивающая сила Архимеда (равная весу вытесненной шариком жидкости):

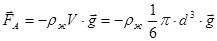; [3]

3. Сила внутреннего трения, определяемая законом Стокса:

, [4]

где - вектор скорости движения шарика.

В первый момент времени, когда сила тяжести превышает сумму выталкивающей силы и силы трения, шарик падает ускоренно. Однако, при увеличении скорости падение возрастает сила вязкого трения. Через некоторое время равнодействующая всех сил, действующих на шарик, становится равной 0;

[5]

и устанавливается постоянная скорость падения. С учетом направления действия сил (рис.2), равенство можно записать в виде:

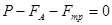. [6]

Подставляя [2], [3] и [4] в выражение [6] находим коэффициент вязкости :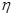

[7]

где 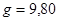– ускорение свободного падения.

Учтем, что скорость равномерного падения шарика в жидкости: , где 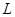– расстояние, пройденное шариком (рис. 2.), 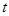– время его падения. Тогда получим:

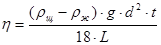[8]