Теоретическое введение. Идеальным газом называется система молекул, которые находятся в непрерывном хаотическом движении и между ними отсутствуют силы межмолекулярного

Идеальным газом называется система молекул, которые находятся в непрерывном хаотическом движении и между ними отсутствуют силы межмолекулярного взаимодействия. Вдали от области фазовых превращений реальные газы можно считать идеальными.

Число параметров, определяющих положение и ориентацию молекул газа в пространстве, будем называть числом ее степеней свободы - .

Согласно положению о равнораспределении энергии по степеням свободы, на каждую степень свободы молекулы приходится энергия равная: , поэтому средняя энергии молекулы газа, должна равняться:

[1]

где - сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы, - постоянная Больцмана.

Для молекул с жесткими межатомными связями (нет колебательных степеней свободы) имеем:

1. Одноатомная молекула - 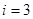(три поступательные степени свободы).

2. Двухатомная молекула - (три поступательные и две вращательные степени свободы).

3. Трехатомная молекула - 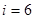(три поступательные и три вращательные степени свободы).

Внутренняя энергия одного моля идеального газа, содержащего молекул, равна:

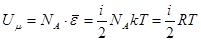[2]

где - универсальная газовая постоянная. Для (где 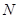- общее число молекул) молей газа имеем:

[3]

Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона) связывает 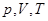- давление, объем и абсолютную температуру газа:

[4]

где 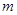- масса газа, – молярная масса газа (масса одного моля).

Теплоёмкостью тела называется величина, численно равная количеству теплоты , которую необходимо ему сообщить, чтобы изменить температуру на один градус Кельвина:

[5]

где 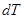- изменение температуры тела, – количество теплоты, сообщённое телу.

Поделив [5] на массу газа 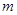и на молярную массу , получим, соответственно удельную и молярную теплоемкости:

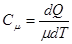; [6]

Для определения теплоёмкости идеального газа воспользуемся первым началом термодинамики, согласно которому количество теплоты - , переданное системе затрачивается на изменение её внутренней энергии и совершение системой работы 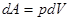против внешних сил:

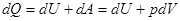[7]

Из выражения [7], следует, что величина теплоемкости зависит от способа нагревания:

Изохорный процесс:

При изохорном процессе изменение объема , в этом случае с учётом равенств [7] и [3] получим величину теплоёмкости при постоянном объеме:

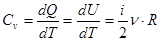или [8]

Изотермический процесс:

В этом случае изменение температуры , и первое начало термодинамики имеет вид:

Так как, температура не меняется, теплоемкость 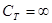. Изотермический процесс описывается уравнением Бойля-Мариотта:

[9]

Изобарный процесс: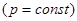

При изобарном процессе:

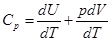[10]

После дифференцирования уравнения Менделеева-Клайперона [4] при постоянном давлении получим:

[11]

Выражение [11] позволяет выяснить физический смысл универсальной газовой постоянной: она численно равна работе совершаемой одним молем идеального газа при повышении его температуры на 1К, при изобарном процессе.

Подставив [11] в [10] и, учитывая [8] найдем теплоемкость при изобарном процессе:

[12]

Разделив [12] на число молей , получим уравнение Майера, связывающее молярные теплоёмкости идеального газа (теплоёмкости одного моля вещества):

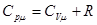[13]

Поделив [12] на [8], найдем отношение теплоемкостей 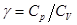(коэффициент Пуассона) для идеального газа:

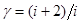[14]

Используя [14], находим теоретические значения для идеальных газов:

для одноатомного ,

для двухатомного ,

для трехатомного идеального газа .

Для экспериментального определения этого отношения Клеман и Дезорм предложили метод адиабатического сжатия.

Адиабатическимназывается процесс, протекающий без теплообмена с окружающей средой 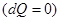, для такого процесса первое начало термодинамики, с учетом [8] имеет вид:

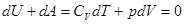[15]

отсюда следует, что при адиабатическом изменении объема газ совершает работу за счёт изменения своей внутренней энергии. Поэтому при таком процессе температура газа изменяется: при сжатии повышается, а при расширении уменьшается.

Решая совместно [15] и [4] можно получить уравнение Пуассона для адиабатического процесса:

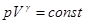[16]

Для определения по методу Клемана-Дезорма нужно осуществить замкнутый процесс (цикл), диаграмма которого приведена на рис. 1.

Уравнение Пуассона для адиабатического сжатия кривая (1-2):

[17]

при этом температура и давление газа увеличиваются до и , соответственно. Если при постоянном объеме температуру уменьшить до первоначального значения , то давление уменьшится от до , (отрезок 2-3). При последующем изотермическом процессе 3-1, который описывается выражением [9], газ возвращается в исходное состояние.

[18]

возведем равенство [18] в степень и разделим его на равенство[17]. После сокращения на получим:

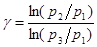или [19]

Описание установки и расчетные формулы

Для осуществления метода Клемана-Дезорма используется прибор (рис. 2) состоящий из большого стеклянного баллона Б, соединенного с насосом Н и водяным манометром М. на пробке баллона имеется клапан К, при открытии которого баллон сообщается с атмосферным воздухом. Клапан открывается рычагом. Если при открытом клапане К медленно откачать из баллона воздух, то температура в нем изменится, а давление будет меньше атмосферного 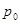на величину , т.е.

[20]

это состояние соответствует точке 1 (рис. 1). Величина измеряется манометром М, по разности уровней жидкости в манометре h. Для осуществления адиабатического процесса 1-2 нужно на короткое время открыть клапан К, при этом давление воздуха в баллоне сравняется с атмосферным.

Если после откачивания в баллоне объемом 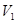остается масса воздуха m, то при открывании клапана в баллон войдёт дополнительная порция воздуха, а масса m займет меньший объем при давлении . Т.к. процесс кратковременный и заметного теплообмена газа в баллоне с окружающей средой нет, то процесс можно считать близким к адиабатному. После адиабатического сжатия (кривая 1-2) температура воздуха в баллоне повышается до (точка 2).

В результате теплообмена температура газа в баллоне через 2-3 мин. практически станет равной комнатной, а давление будет меньше атмосферного (точка 3):

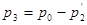[21]

процесс теплообмена (2-3) происходит при постоянном объеме. Конечное состояние этого процесса соответствует точке 3. т.к. точки 1 и 3 соответствуют одинаковой температуре, то они должны лежать на одной изотерме, для которой выполняется выражение[18].

Т.к. давление измеряется жидкостным манометром, то и формулы [20] и [21] можно заменить на значения давления в мм водяного столба:

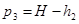и [22]

Для определения через и подставим последние выражения в [19] и разложим 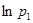и в ряд Тейлора и, ограничиваясь первыми двумя членами разложения, получим :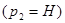

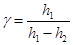[23]

значения , найденные по формуле [23], сильно зависят от времени, на которое открывается клапан 3. это связанно с тем, что чем меньше время, тем меньшее количество теплоты отдает газ, через стенки сосуда и тем ближе процесс к адиабатическому, а измеренное значение ближе к истинному.