
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение.
Под действием сил, происходит деформация тел, т. е. изменение их размеров и формы. Если после прекращения действия сил, тело принимает первоначальный размер и форму, деформация называется упругой. Упругие деформации происходят в том случае, если сила, приложенная к телу, не превосходит некоторый, определенный для каждого тела предел. При превышении этого предела тело получает остаточные или пластические деформации, сохраняющиеся и после прекращения действия силы на тело.
Величина, равная отношению силы к величине поверхности, на которую действует сила, называется напряжением. Благодаря взаимодействию частей тела друг с другом напряжение передается во все точки тела, и весь объем тела оказывается в напряженном состоянии. Если сила направлена по нормали к поверхности, напряжение называется нормальным 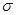 . Если сила направлена по касательной к поверхности, напряжение называется тангенциальным
. Если сила направлена по касательной к поверхности, напряжение называется тангенциальным  .
.
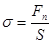 и
и 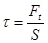 [1]
[1]
В пределах упругости, величина относительной деформации 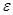 тела пропорциональна, приложенному напряжению (закон Гука):
тела пропорциональна, приложенному напряжению (закон Гука):
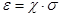 или
или 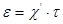 [2]
[2]
где 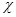 и
и  - коэффициенты пропорциональности, определяемые формой, размерами и материалом, из которого изготовлено тело.
- коэффициенты пропорциональности, определяемые формой, размерами и материалом, из которого изготовлено тело.
Все возможные виды упругих деформаций твердого тела (растяжение, сжатие, сдвиг, изгиб, кручение), могут быть сведены к двум основным: растяжению (или сжатию) и сдвигу.
Деформация растяжения (или сжатия).
 Если к противоположному концу, закрепленного однородного стержня (рис. 1), длиной
Если к противоположному концу, закрепленного однородного стержня (рис. 1), длиной 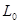 и постоянного сечения
и постоянного сечения 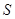 приложить направленную вдоль его оси силу
приложить направленную вдоль его оси силу  , то длина стержня получит приращение
, то длина стержня получит приращение 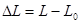 , где
, где 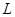 - новая длина стержня. Величина:
- новая длина стержня. Величина: 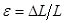 является мерой относительной деформации тела.
является мерой относительной деформации тела.
В пределах упругой деформации величина относительной деформации 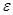 пропорциональна приложенному нормальному напряжению (закон Гука):
пропорциональна приложенному нормальному напряжению (закон Гука):
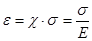 или
или  [3]
[3]
где  - модуль Юнга, численно равный нормальному напряжению, удлиняющему стержень в два раза
- модуль Юнга, численно равный нормальному напряжению, удлиняющему стержень в два раза 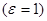 . Учитывая, что
. Учитывая, что 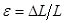 , перепишем [3] в виде:
, перепишем [3] в виде:
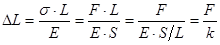 или
или 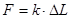 [4]
[4]
где 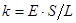 - коэффициент жесткости или просто жесткость тела.
- коэффициент жесткости или просто жесткость тела.
Деформация сдвига.
Сдвигом называется деформация, при которой все плоские слои твердого тела, параллельные некоторой плоскости (плоскости сдвига), смещаются параллельно друг другу (рис. 2).
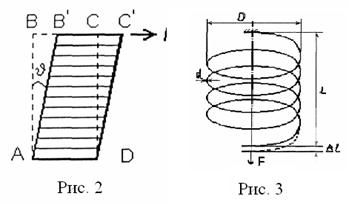
Сдвиг происходит под действием силы  , приложенной параллельно плоскости сдвига ВС. Мерой относительной деформации при этом является тангенс угла сдвига
, приложенной параллельно плоскости сдвига ВС. Мерой относительной деформации при этом является тангенс угла сдвига 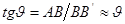 (относительный сдвиг).
(относительный сдвиг).
При упругих (обратимых) деформациях, относительный сдвиг пропорционален касательному напряжению (выполняется закон Гука):
 [5]
[5]
где S - площадь грани ВС, G - модуль сдвига, численно равный касательному напряжению, вызывающему относительный сдвиг, равный единице.
В данной работе определяется модуль сдвига материала, из которого изготовлена винтовая пружина (рис. 3), основными геометрическими параметрами которой являются, диаметр проволоки d, диаметр витка пружины D и число витков N.
Под действием растягивающей силы F, перпендикулярной виткам, длина пружины L увеличивается согласно закону Гука [4] на величину
 [6]
[6]
где k- жесткость пружины.
Удлинение пружины 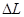 , складывается из деформаций сдвига по всей длине проволоки, из которой она изготовлена и определяется растягивающей силой, модулем сдвига и геометрическими размерами пружины:
, складывается из деформаций сдвига по всей длине проволоки, из которой она изготовлена и определяется растягивающей силой, модулем сдвига и геометрическими размерами пружины:
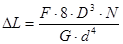 [7]
[7]
Решая совместно [6] и [7], находим связь между модулем сдвига  и жесткостью пружины
и жесткостью пружины  :
:
 [8]
[8]
Пружинный маятник.
Пружинным маятником будем называть тело, подвешенное к пружине, жестко закрепленной верхним концом к неподвижной опоре, и способное совершать колебания в вертикальной плоскости под действием силы тяжести (рис. 4).
На тело, массой 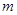 , подвешенное на пружине действуют две силы: постоянная по величине сила тяжести
, подвешенное на пружине действуют две силы: постоянная по величине сила тяжести 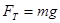 , определяющая длину пружины в состоянии равновесия
, определяющая длину пружины в состоянии равновесия 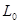 и сила упругости пружины, выражаемая законом Гука, в виде:
и сила упругости пружины, выражаемая законом Гука, в виде:  , где
, где 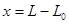 - величина отклонения тела от положения равновесия. Уравнение движения тела (второй закона Ньютона):
- величина отклонения тела от положения равновесия. Уравнение движения тела (второй закона Ньютона):
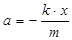 или
или 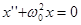 [9]
[9]
где 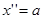 - ускорение тела,
- ускорение тела,  - собственная частота колебания маятника. Решение данного уравнения:
- собственная частота колебания маятника. Решение данного уравнения:
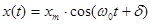 , [10]
, [10]
где  – амплитуда колебаний (максимальный угол отклонения от вертикали),
– амплитуда колебаний (максимальный угол отклонения от вертикали),  - начальная фаза колебания. Таким образом, пружинный маятник совершает гармонические колебания с частотой
- начальная фаза колебания. Таким образом, пружинный маятник совершает гармонические колебания с частотой  и периодом:
и периодом:
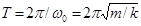 [11]
[11]
Описание установки и расчетные формулы
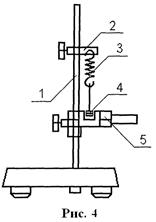
Для определения модуля сдвига в работе используется пружинный маятник, показанный на рис. 3.
На штативе 1 установлен кронштейн 2 с узлом крепления вертикально подвешенных сменных пружин 3. К пружине подвешивается наборный груз 4. Измерение периодов колебаний груза производится с помощью фотодатчика 5.
Выведенный из положения равновесия груз массой m совершает гармонические колебания [10] с периодом  .
.
Используя [11], выразим жесткость пружины через период колебаний маятника:
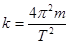 [12]
[12]
Подставив [12] в [8], находим формулу для расчета модуля сдвига материала, из которого изготовлена пружина:
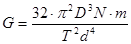 [13]
[13]
Таким образом, измерив, период колебаний и воспользовавшись формулой [13], можно найти модуль сдвига  .
.
Интервал надежности.
Интервал надежности можно оценить по правилам расчета погрешности косвенного измерения:
 [14]
[14]
где  - коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.
- коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.
Записываем результат в виде: 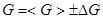 ; p = ;
; p = ;
2. Выполнение работы.
Приборы и принадлежности:
1. Штатив с кронштейном и фотодатчиком
2. Электронный таймер.
3. Пружина
4. Груз и добавочные грузы.
5. Штангенциркуль.
Кронштейн 2 с вертикально подвешенной пружиной 3 закрепить на вертикальной стойке 1 таким образом, чтобы наборный груз 4, подвешенный к пружине, своей нижней плоскостью закрывал оптическую ось фотодатчика 5 на 2-3 мм (оптическая ось совпадает с рисками на фотодатчике).
1. Измерить все параметры пружины D, d, N.
2. Оттянуть груз вниз на 3-5 мм и отпустить. При этом груз начинает совершать колебательные движения на пружине. Измерить время 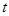 для
для 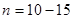 полных колебаний маятника. По формуле
полных колебаний маятника. По формуле 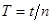 рассчитать период колебаний
рассчитать период колебаний  .
.
3. Повторить пункт 2 не менее трех раз, записывая данные в таблицу результатов.
4. Повторить задание п. 2 – 3 не менее трех раз, увеличивая массу груза m. Все полученные данные занести в таблицу результатов.
5. Для каждого значения m вычислить модуль сдвига G(m) по формуле [13] и записать в таблицу результатов.
6. Найти среднее значение:  , где
, где 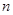 - число измерений с разными значениями массы груза
- число измерений с разными значениями массы груза 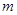 . По формуле [14], оценить интервал надежности и записать результат измерений в виде:
. По формуле [14], оценить интервал надежности и записать результат измерений в виде: 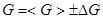 в последнюю строку таблицы.
в последнюю строку таблицы.
Таблица результатов.
| Параметры пружины | 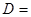 , мм , мм
| 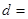 , мм , мм
| 
| |
| № опыта | 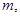 г г
| 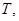 с с
| 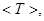 с с
| 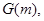 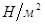
|
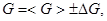 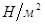
| 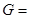 , p = ; , p = ;
|
Контрольные вопросы.
1. Виды деформаций.
2. Нормальное и тангенциальное напряжение. Единицы измерения.
3. Сформулируйте закон Гука.
4. Деформация растяжения. Модуль Юнга. Единицы измерения.
5. Деформация сдвига. Модуль сдвига. Единицы измерения.
6. Растяжение пружины. Связь модуля сдвига и жесткости пружины.
7. Пружинный маятник. Уравнение колебаний. Частота и период колебаний.
8. Как в данной работе определяется модуль сдвига? Расчетная формула.
Литература.
Курс общей физики под ред. Савельева И. В. т. 1.
Лабораторная работа № 11. Определение модуля Юнга по стреле прогиба прямоугольной пластины.
Цель работы – Определение модуля Юнга по стреле прогиба пластины.
Дата добавления: 2014-10-31; просмотров: 313; Мы поможем в написании вашей работы!; Нарушение авторских прав |