Теоретическое введение. Для характеристики инерционности тела при вращении вводятся понятия момента инерции материальной точки массы m

Для характеристики инерционности тела при вращении вводятся понятия момента инерции материальной точки массы m, находящейся на расстоянии r от оси вращения и момент инерции тела , равный сумме моментов инерции всех материальных точек составляющих тело - сумме произведений масс этих точек на квадрат расстояния до оси :

[1]

Нахождение момента инерции во многих случаях значительно облегчается при использовании теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния между осями:

[2]

Моментом силы относительно некоторой точки “O” называется векторная величина , определяемая выражением

[3]

где – радиус-вектор, проведенный из точки “O” в точку приложения силы.

Направление вектора M определяется по правилу правого винта. Момент силы направлен вдоль оси вынуждаемого вращения (он не имеет конкретной точки приложения, как обычные вектора), т.е. является аксиальным псевдовектором.

Основной закон динамики вращательного движения (аналог второго закона Ньютона) связывает результирующий момент сил , действующих на тело и его угловое ускорение (аналог линейного ускорения):

или [4]

где J – момент инерции тела, относительно оси вращения, определяемый выражением [1],

Импульсом теланазывается вектор, равный произведению массы тела на его скорость движения:

. [5]

Моментом импульса материальной точки, относительно данной оси, называется вектор, определяемый векторным произведением радиус-вектора точки на его импульс :

. [6]

Модуль момента импульса точки, относительно оси равен:

где - кратчайшее расстояние от точки до оси, - момент инерции точки, относительно оси, 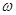- угловая скорость вращения.

Полная механическая энергия тела, массой 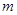, мо­жет быть представлено как сумма кинетических энергий его поступательного и вращательного движений и потенциальной энергии взаимодействия с другими телами:

[7]

где - кинетическая энергия поступательного, - кинетическая энергия его вращательного движения, а - потенциальная энергия.

Законы сохранения в механике

В замкнутой системе 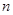материальных тел, векторная сумма импульсов тел сохраняется– закон сохранения импульса (при этом векторная сумма всех внешних сил равна нулю):

Если , то [8]

В замкнутой консервативной системе (при отсутствии потерь на преодоление сил сопротивления) сумма их полных механических энергий [7] сохраняется - закон сохранения полной механической энергии.

Если суммарный момент внешних сил, действующих на систему, относительно какой-либо оси равен нулю, то суммарный момент импульса такой системы материальных точек, относительно данной оси сохраняется – закон сохранения момента импульса:

Если , то [9]

В данной работе рассматривается система двух тел: «пуля» и рама крутильного маятника. Суммарный момент внешних сил в этом случае равен нулю и выполняется закон сохранения суммарного момента импульса.

Крутильный маятник

Крутильным маятником называется тело (рама на рис. 1), подвешенное на упругой нити, которая натянута между двумя неподвижными опорами (унифилярный подвес), и способное совершать крутильные колебания в плоскости перпендикулярной нити.

Так как момент сил тяжести и силы натяжения нити, относительно оси вращения маятника равны нулю, результирующий момент равен моменту силы упругости нити (закон Гука):

, [10]

где - модуль кручения нити. Величина D зависит от длины проволоки, её диаметра и модуля сдвига, характеризующего упругие свойства материала проволоки. Знак минус в [10], учитывает противоположность направлений вращательного момента и угла закручивания нити маятника.

Подставляя [10] в [4], и учитывая, что угловое ускорение , где - вторая производная по времени угла закручивания нити, получим:

[11]

Поделим уравнение [11] на и перенесем все слагаемые влево:

,

где - собственная частота колебания маятника. Решение данного уравнения:

,

где – амплитуда (максимальный угол закручивания нити), - начальная фаза колебания.

Таким образом, крутильный маятник совершает гармонические колебания с частотой и периодом . [12]

При крутильных колебаниях, происходит преобразование кинетической энергии вращательного движения тела в потенциальную энергию упругости нити, и обратно. Полная энергия маятника (без учета потерь энергии на сопротивление среды) в любой момент времени равна их сумме:

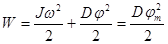[13]

Описание установки и расчетные формулы.

Основным элементом установки (рис. 1) является крутильный маятник. «Пулей» служит тонкое металлическое кольцо 1. К стойке на кронштейне крепится «пистолет» 2, состоящий из направляющего стержня с пружиной и спускового устройства. К стойке также на кронштейне крепится фотодатчик 3, соединенный с электронным блоком регистрации времени и числа колебаний (на рисунке не показан).

После выстрела «пуля» 1 попадает в «мишень» 4 и прилипает к ее поверхности. Соударение пули с мишенью происходит за столь короткое время, что действием момента сил упругости нити за это время можно пренебречь. Сумма моментов внешних сил, действующих на рамку (сил тяжести и натяжения нити) относительно вертикальной оси равны нулю.

Момент импульса «пули», относительно оси вращения рамки до соударения: , где т - масса «пули», - его скорость, l – прицельное расстояние (рис. 2).

Момент импульса рамки маятника, относительно оси вращения после соударения: , где - момент инерции рамки, относительно оси вращения, 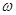- угловая скорость вращения рамки.

По закону сохранения момента импульса системы: «пуля» - маятник, имеем: L₁ = L₂, следовательно:

. [14]

Чтобы воспользоваться этой формулой, нужно найти угловую скорость рамки 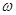, после удара и момент инерции рамки , относительно оси вращения:

[15]

где - моменты инерции рамки с грузами и без грузов, М - масса каждого из грузов, l₁ – расстояние грузов от оси вращения. Выражение [15], является следствием теоремы Штейнера[2]. Вкладом в момент инерции прилипшей «пули» пренебрегаем, из-за малости его массы.

Момент инерции рамки с грузами можно найти из измерений периода колебаний рамки с грузами и без них .

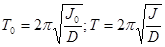[16]

где D - модуль кручения проволоки.

Исключая модуль кручения D из формул [16], находим момент инерции рамки с грузами:

. [17]

Для нахождения угловой скорости вращения маятника 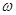воспользуемся законом сохранения энергии, полученноймаятником после удара. Приравняв, кинетическую энергию вращательного движения рамки после удара потенциальной энергии закрученной нити , находим угловую скорость рамки сразу после удара :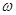

[18]

Подстановка соотношений [17] и [18] в уравнение [14] дает окончательную формулу:

[19]

Интервала надежности полученного значения можно оценить по правилам расчета погрешности косвенного измерения:

[20]

где - коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.

Записываем результат в виде: ; p = ;