Теоретическое введение. Материальные точки с массами m1 и m2, находящиеся на расстоянии r друг от друга взаимодействуют по закону всемирного тяготения

Материальные точки с массами m₁ и m₂, находящиеся на расстоянии r друг от друга взаимодействуют по закону всемирного тяготения, установленного Ньютоном:

[1]

где - гравитационная постоянная.

Закон тяготения в форме [1] справедлив и для сферически однородных протяженных тел, в частности, его можно использовать при вычислении силы тяготения тел к Земле:

, [2]

где M_з и R_з – масса и радиус Земли, соответственно, h – расстояние тела массой m от поверхности Земли (высота), g – ускорение свободного падения.

Ускорение g, приобретаемое свободно падающим на Землю телом, с учетом [2], равно:

[3]

и, направлено вертикально вниз, к центру Земли.

Вблизи поверхности Земли (h = 0) среднее (стандартное) значение ускорения свободного падения равно g = 9,80 м/с². Сплюснутость Земли и ее вращение (неинерциальность системы отсчета, связанной с Землей) приводят к отличию ускорение свободного падения (и, следовательно, силы тяжести) на экваторе (g ≈9,78 м/с²) и на полюсе (g ≈9,83 м/с²). Вращение Земли приводит также к зависимости ускорения свободного падения от широты местности.

Математическим маятником называется тело малых размеров (материальная точка), подвешенное к неподвижной опоре на невесомой нерастяжимой нити, и способное совершать колебания в вертикальной плоскости под действием силы тяжести (рис. 1).

Основной закон динамики вращательного движения (аналог второго закона Ньютона) связывает результирующий момент сил , действующих на тело и его угловое ускорение (аналог линейного ускорения):

или [4]

где J – момент инерции тела, относительно оси вращения.

Так как момент силы натяжения нити T , относительно оси вращения маятника равен нулю, результирующий момент равен моменту силы тяжести:

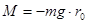, [5]

где - плечо силы тяжести. Знак минус в [5], учитывает противоположность направлений вращательного момента и угла отклонения маятника от вертикали.

Подставляя [5] в [4], и учитывая, что момент инерции материальной точки, относительно оси вращения равен: , а его угловое ускорение , где - вторая производная по времени угла отклонения нити от вертикали, получим:

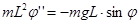[6]

Для малых углов отклонения маятника, при которых дифференциальное уравнение движения маятника запишется в виде (предварительно, уравнение [6] поделим на и перенесем все слагаемые влево):

, [7]

где - собственная частота колебания маятника. Решение данного уравнения:

, [8]

где – амплитуда колебаний (максимальный угол отклонения от вертикали), - начальная фаза колебания. Таким образом, при малых амплитудах математический маятник совершает гармонические колебания с частотой 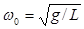и периодом 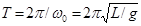. Откуда:

[9]

Физическим маятником называется твердое тело, имеющее возможность совершать колебания под действием силы тяжести вокруг неподвижной горизонтальной оси (точка 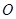на рис. 2), не проходящей через центр массы тела (точка ).

Повторяя предыдущий вывод, и учитывая, что момент силы тяжести, относительно оси вращения 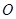равен: , где - плечо силы, момент инерции маятника, относительно той же оси - , находим уравнение колебаний:

Для малых углов отклонения маятника, при которых дифференциальное уравнение движения маятника запишется в виде

Частота и период малых колебаний физического маятника:

и

Приравняв выражения для периодов колебаний математического и физического маятников, находим приведенную длину физического маятника:

Описание установки и расчетные формулы

Схема установки показана на рис.3. В качестве математического маятника используется металлический шар 1, подвешенный на двух капроновых нитях к кронштейну 2. На этом же кронштейне находится ролик 3, позволяющий изменять длину маятника. На нижнем кронштейне укреплен фотодатчик 4. Расстояние между кронштейнами определяется по нанесенной на штатив шкале 5.

Для экспериментального определения ускорения свободного падения перепишем соотношение [9] в следующем виде:

[10]

где - коэффициент пропорциональности между квадратом периода и длиной маятника (тангенс угла наклона графика зависимости ).

Изменяя длину маятника L, и определяя периоды его колебаний, находим ряд точек (L_i; T_i). Строим точки на графике , откладывая по вертикальной оси квадраты периодов колебаний 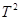, а по горизонтальной оси, соответствующие им длины маятника 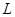. Следуя рекомендациям пографическому определению параметров прямой линии, приведенным во введении в разделе «Графическая обработка результатов измерений», проводим наилучшую прямую. По графику функции определяем тангенс угла наклона и экспериментальное значение ускорения свободного падения :

[11]

Интервала надежности полученного значения можно оценить по правилам расчета погрешности косвенного измерения:

[12]

где - коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.

Записываем результат в виде: ; p = ;