Теоретическое введение. Материальная точка – тело, размерами которого можно пренебречь, в условиях данной задачи

Материальная точка – тело, размерами которого можно пренебречь, в условиях данной задачи. Для описания положения материальной точки в каждый момент времени, необходимо выбрать систему отсчета – совокупность таймера, тела отсчета и жестко связанную с ним систему координат. В общем случае движение материальной точки, в выбранной системе отсчета, описывается мгновенным значением радиус-вектора или координат (кинематическими уравнениями движения):

или:

Линия, описываемая движущейся в пространстве точкой, называется траекторией, которая может быть прямолинейной или криволинейной.

Длина участка траектории, пройденного телом за промежуток времени 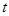называется длиной пути и является скалярной функцией от времени: .

Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется перемещением . При прямолинейном равномерном движении модуль перемещения равен пройденному пути

Для характеристики движения вводится векторная величина – скорость . Вектором средней скорости называется отношение перемещения точки к промежутку времени , за который это перемещение произошло:

[1]

При средняя скорость стремится к предельному значению – производной перемещения по времени, которое называется мгновенной скоростью :

[2]

Если скорость не изменяется с течением времени , то движение называется равномерным. В этом случае (при движении тела вдоль оси x):

, [3]

где - координата точки в начальный момент времени.

При неравномерном движении, аналогично [1] и [2], вводят понятие векторов среднего и мгновенного ускорения :

и [4]

Если ускорение не изменяется во времени , то движение называется равноускоренным. В этом случае (при прямолинейном движении тела вдоль оси x):

и [5]

где и - координата и скорость точки в начальный момент времени .

Состояние движения тела (скорость и ускорение) может измениться только в результате взаимодействия с другими телами, мерой которого является вектор силы , и может быть установлено, при помощи законов Ньютона:

1. Всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока векторная сумма, действующих на него сил равна нулю, т. е.:

a. , если [6]

2. Ускорение, приобретаемое телом, прямо пропорционально векторной сумме сил, действующих на него, и обратно пропорционально массе тела (где - импульс тела, m = const.):

a. или [7]

3. Все тела, при взаимодействии друг с другом, действуют друг на друга с равными по величине и противоположно направленными силами:

[8]

Описание установки и расчетные формулы.

Для проверки законов прямолинейного движения в данной работе используется машина Атвуда, схема которого изображена на рис. 1.

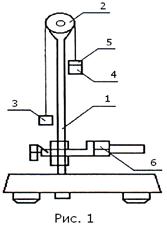Машина Атвуда состоит из укрепленного на штативе 1 блока 2, через который перекинута нить с подвешенными на ней одинаковыми грузами 3 и 4. Масса этих грузов может быть увеличена добавочными небольшими грузами (перегрузками) 5. На верхнем кронштейне установлен также электромагнитный тормоз, предназначенный для фиксации исходного положения грузов. Установка работает от блока электронного ФМ 1/1, на передней панели которого расположено табло электронного секундомера, соединенного с фотодатчиком 6.

При одинаковой массе М грузов 3 и 4 система находится в состоянии безразличного равновесия. Если на груз 4 положить перегрузок 5 (массы m), то вся система начнет двигаться равноускоренно, с ускорением .

На груз 3 и груз 4 с перегрузом 5 будут действовать две силы: сила тяжести и сила натяжения нити (рис.2). При этом, если масса блока невелика по сравнению с массой груза М и трение мало, то раскручивание блока практически не требует приложения к нему крутящего момента, и силы натяжения нити по обе стороны блока равны.

Применив второй закона Ньютона к каждому грузу можно записать уравнения движения системы (все силы, направленные так же как вектор ускорения, считаем положительными):

где а – ускорение системы, Т – натяжение нити, g – ускорение свободного падения.

Решение системы уравнений дает:

[9]

С другой стороны, полагая в [5] и , находим:

или [10]

где , коэффициент пропорциональности между и величиной перемещения грузов h (тангенс угла наклона графика функции , см. Введение, §1).

Теоретическое значение ускорения грузов, рассчитанное по формуле [9], можно сравнить с экспериментальным значением [10].

Изменяя величину перемещения грузов h и измеряя время движения t, находим ряд точек . Строим точки на графике , откладывая по горизонтальной оси , по вертикальной оси . Если кинематическое уравнение [10] выполняется, то экспериментальные точки должны хорошо ложиться на прямую линию, исходящую из начала координат.

Следуя рекомендациям пографическому определению параметров прямой линии, приведенным во введении в разделе «Графическая обработка результатов измерений», проводим наилучшую прямую, определяем тангенс угла ее наклона к горизонтальной оси и находим величину экспериментального ускорения грузов :

[11]

Интервала надежности полученного значения (рис. 3) можно оценить по правилам расчета погрешности косвенного измерения, зная инструментальную погрешность определения расстояния h (миллиметровая линейка, мм ) и погрешность определения времени t (электронный таймер, с):

[12]

где - коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.

Записываем результат в виде: ; p = ;