Расчет погрешности прямых измерений

Прежде, чем приступить к измерениям, необходимо предварительно определить пределы точности данных приборов (инструментальные погрешности ).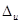

Равноточные измерения любой физической величины делаются не менее трех раз и заносятся в таблицу, с учетом инструментальной погрешности. В зависимости от поведения значений результатов измерения, возникают две различные схемы:

Случайная погрешность много меньше инструментальной

Если оказывается, что все время получается один и тот же результат (нет разброса), то в качестве интервала надежности берется стандартная (инструментальная) погрешность прибора ∆_и, рассчитанная по его классу точности (или погрешность градуировки прибора) и результат записывается в виде:

При этом доверительная вероятность (надежность) равна и, как правило, не указывается.

Случайная погрешность сравнима с инструментальной

Если разброс значений физической величины x превышает погрешность градуировки, то количество измерений n увеличивают до тех пор, пока они не окажутся величинами одного порядка. Интервал надежности вычисляют в следующей последовательности:

1. Находят среднее значение:

2. Оценивают среднеквадратичное отклонение - СКО:

3. По заданному значению надежности p и числу измерений n, находят случайную составляющую погрешности:

4. Полную погрешность вычисляют как корень квадратный из суммы квадратов случайной ∆х_сл и инструментальной ∆x_и составляющих:

5. Находят относительную погрешность:

6. Результат записывают в виде: , , р = …