Точность измерений

Виды измерений. Абсолютная и относительная погрешность

Измерения могут быть прямыми, при которых значения физической величины находят непосредственным отсчетом по шкале измерительного прибора (измерение длины линейкой, температуры термометром) и косвенными, при которых значение физической величины находят на основании известной зависимости между этой величиной и величинами, измеряемыми непосредственно (определение плотности тела по отношению массы к объему, определение сопротивления проводника по отношению разности потенциалов к току и т. д.).

В зависимости от числа проведенных измерений различают однократные и многократные измерения.

Многократные измерения могут быть равноточными и неравноточными. Равноточными называют измерения, выполненные с одинаковой точностью (например, одним и тем же прибором, при одинаковых условиях).

Измерения могут быть прямыми и косвенными, однократными и многократными, равноточными и неравноточными, результаты измерений физических величин всегда являются приближенными числами . Многократные измерения записываются в таблицу с обязательным указанием единиц измерения.

Точностьпроведенного измеренийне может превышать точность прибора,которым проводилось измерение и характеризуется двумя основными параметрами: абсолютной и относительной погрешностями.

Для характеристики каждого конкретного измерения используют его абсолютную погрешность, т.е. модуль разности между истинным значением величины и ее значением, полученным в результате измерения:

[1.1]

На практике часто истинное значение неизвестно, поэтому приходится использовать вместо него арифметическое среднее из нескольких измерений, при этом сама абсолютная погрешность также становится приближенным числом.

Абсолютная погрешность не в полной мере характеризует результат измерения. Пусть, например, в результате измерений установлено, что длина стола равна L = (100 ±1) см, а толщина его крышки d = (2 ±1) см. Хотя абсолютная погрешность измерений в этих двух случаях одинакова, ясно, что качество измерений в первом случае выше.

Качество измерений характеризуется относительной погрешностью ε, равной отношению абсолютной погрешности к значению величины х_изм , получаемой в результате измерения:

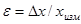[1.2]

Абсолютная погрешность [1.1] показывает, насколько истинное значение измеряемой величины отличается от измеренного значения.

Относительная погрешность [1.2] характеризует качество измерения, т.е. насколько верно подобрано соотношение измеряемой величины и абсолютной погрешности измерения.