Теоретическое введение. Плотностью элементарной части тела называется предел отношения элементарной массы ∆m к элементарному объему ∆V

Плотностью элементарной части тела называется предел отношения элементарной массы ∆m к элементарному объему ∆V, при ∆V→ 0:

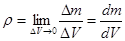[1]

Для однородного тела ( 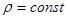) определение плотности сводится к нахождению отношения его массы к объему: .

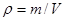Внимание! Для экспериментального определения плотности тел правильной геометрической формы (цилиндр и параллелепипед) в данной работе необходимо предварительно провести прямые измерения их линейных размеров и массы, пользуясь рекомендациями, приведенными во введении §1. Раздел: «Расчет погрешности прямых измерений».

Доверительной вероятностью (надежностью) P(∆x) серии измерений называется вероятность попадания истинного значения измеряемой величины в данный интервал (выражается в долях единицы или в процентах).

Интервал (<x>± ∆x) в который попадает истинное значение искомой величины с заданной доверительной вероятностью, называют доверительным интервалом (интервалом надежности).

Определение плотности цилиндра.

Плотность однородного цилиндрического тела можно рассчитать по формуле:

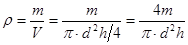, [2]

где d – диаметр цилиндра, h – его высота.

Для нахождения относительной погрешности косвенного определения плотности цилиндра, прологарифмируем расчетную формулу:

и возьмем дифференциал. Заменив дифференциалы приращениями, получим:

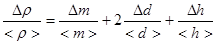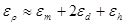или , [3]

где - средние значения массы, диаметра и высоты, найденные в результате прямых измерений, соответственно, а 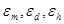- относительные погрешности их прямых измерений.

Среднее значение плотности можно найти, подставляя в расчетную формулу [2] средние значения массы, диаметра и высоты:

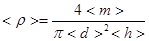[4]

Определение плотности параллелепипеда.

Плотность однородного тела в форме параллелепипеда можно рассчитать по формуле:

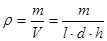, [5]

где l – длина тела , d –ширина тела, h – его высота. Действуя аналогично предыдущему случаю, находим:

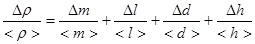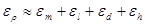или , [6]

где - средние значения массы, длины, ширины и высоты, найденные в результате прямых измерений, соответственно, а - относительные погрешности их прямых измерений.

Среднее значение плотности:

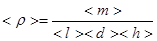[7]

Интервал надежности 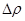при определении плотности во всех случаях, можно вычислить по формуле:

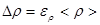[8]

где - относительная погрешность определения плотности, вычисляемая по формуле [3] для цилиндра, или по формулу [6] для параллелепипеда.

Результат записывается в виде:

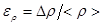, при р = , , [9]

где величина надежности p принимается равной наименьшей надежности прямых измерений массы и линейных размеров.