Теоретическое введение. Для описания кинематики вращательного движения тела, по аналогии с кинематикой поступательного движения (см

Для описания кинематики вращательного движения тела, по аналогии с кинематикой поступательного движения (см. теоретическое введение к предыдущей работе), вводятся понятия углового перемещения (угла поворота радиус-вектора r) , угловой скорости вращения и углового ускорения . Связь между линейными и угловыми величинами, описывающими движение данной точки вращающегося тела, даются выражениями:

и [1]

Для характеристики инерционности тела при вращении вводятся понятия момента инерции материальной точки массы m, находящейся на расстоянии r от оси вращения и момент инерции тела , равный сумме моментов инерции всех материальных точек составляющих тело - сумме произведений масс этих точек на квадрат расстояния до оси :

[2]

Нахождение момента инерции во многих случаях значительно облегчается при использовании теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния между осями:

[3]

Для описания вращательного движения под действием той или иной силы важна не только величина силы, но, также то, к какой точке тела она приложена. Поэтому вместо силы f , при вращательном движении используют величину момента силы относительно данной оси вращения:

[4]

где 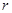- плечо силы, кратчайшее расстояние от линии действия силы до оси вращения.

В зависимости от направления вращения, создаваемой силой, величине момента приписывается знак плюс или минус (в соответствии с правилом правого винта). Если к телу одновременно приложены моменты нескольких сил, то они складываются, с учетом знака.

Основной закон динамики вращательного движения (аналог второго закона Ньютона) связывает результирующий момент сил , действующих на тело и его угловое ускорение (аналог линейного ускорения):

[5]

где J – момент инерции тела, относительно оси вращения, определяемый выражением [2], - момент сил, приложенных к телу, относительно той же оси вращения (определяется выражением [4]).

Описание установки и расчетные формулы.

Для изучения основного закона динамики вращательного движения в данной работе используется маятник Обербека, схема которого изображена на рис. 1.

Маятник состоит из четырех стержней 1, укрепленных во втулке. На стержнях, на расстоянии от оси, закрепляются грузы 2, перемещая которые, можно менять момент инерции маятника. На одной оси с маятником насажены два шкива: большего 3 и меньшего 4 радиуса r. Гиря 5, приводящая тело во вращение, прикреплена к концу нити, которая наматывается на шкив 3 или 4. На основную гирю 5 могут надеваться от одного до четырех дополнительных грузов 6. Для фиксации времени и остановки опускания груза 5, служит фотодатчик 7.

Вращение маятника происходит под действием момента силы натяжения нити М противоположно направлению момента сил трения 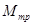. Таким образом, согласно равенству [5] уравнение движения маятника имеет вид:

или [6]

Из равенства [6] видно, что если сила трения постоянна (не зависит от скорости), то зависимость величины М от e является линейной функцией вида: . При этом J играет роль углового коэффициента k. Таким образом, экспериментальное исследование взаимосвязи между моментом силы натяжения М и угловым ускорением e позволяет найти момент инерции маятника J.

Движение гири 5 происходит под действием силы тяжести тg, где т - масса гири; g - ускорение свободного падения, и силы натяжения нити T. Согласно второму закону Ньютона, уравнение движения гири имеет вид:

[7]

Ускорение движения гири а, можно найти, с одной стороны, зная время t её опускания и пройденный путь h, с другой стороны, по значению ε - углового ускорения вращения шкива и r - радиуса шкива.

откуда [8]

Из уравнений [7] и [8] получаем выражение для определения момента силы натяжения нити, относительно оси вращения (массой блока и трением на оси блока пренебрегаем):

[9]

Формулы [8] и [9] позволяют найти, по экспериментальным данным, угловое ускорение e и момент силы натяжения М. Проведя опыты с гирями различной массы m, находим ряд точек . Строим точки на графике , откладывая по вертикальной оси моменты сил натяжения , а по горизонтальной оси, соответствующие им угловые ускорения 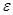. Если формула [6] верна, то экспериментальные точки должны хорошо укладываться на прямую линию. Определение момента инерции маятника сводится к определению углового коэффициента прямой линии, проведенной по найденным точкам.

Следуя рекомендациям пографическому определению параметров прямой линии, приведенным во введении §2, проводим наилучшую прямую и определяем среднюю величину экспериментального значения момента инерции маятника Обербека :

[10]

Интервала надежности полученного значения можно оценить по правилам расчета погрешности косвенного измерения, зная инструментальную погрешность определения h (миллиметровая линейка, мм ) и погрешность определения времени t (электронный таймер, с):

[11]

где - коэффициент Стьюдента, зависящий от выбора интервала надежности (доверительной вероятности) p и числа измерений n.

Записываем результат в виде: ; p = ;