Теоретическое введение. Существует два основных вида движения твердого тела – поступательное и вращательное.

Существует два основных вида движения твердого тела – поступательное и вращательное.

Поступательное движение

При поступательном движении все точки тела полу­чают за один и тот же промежуток времени равные по модулю и направлению перемещения, вследствие чего ско­рости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно опреде­лить движение одной из точек тела (например, его центра масс) для того, чтобы охарактеризовать полностью движе­ние всего тела.

Для описания кинематики поступательного движения тела вводятся понятия перемещения (где и - радиус-векторы конечной и начальной точек, соответственно), скорости и ускорения .

Инерционность поступательного движения тела характеризуется его массой .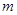

Основной закон динамики поступательного движения тела связывает векторную сумму сил, действующих на тело, с величиной ускорения тела (второй закон Ньютона):

[1]

Полная механическая энергия поступательно движущегося (в поле тяготения Земли) тела, равна сумме его кинетической и потенциальной 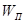составляющих:

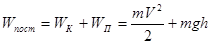[2]

где - ускорение свободного падения, - высота тела от поверхности Земли.

Вращательное движение.

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на од­ной и той же прямой, называемой осью вращения.

Для описания кинематики вращательного движения тела, по аналогии с кинематикой поступательного движения, вводятся понятия углового перемещения (угла поворота радиус-вектора r, начинающегося на оси вращения) , угловой скорости вращения и углового ускорения .

Связь между линейными и угловыми величинами, описывающими движение данной точки вращающегося тела, даются выражениями:

и [3]

Инерционность тела при вращении характеризуется моментом инерции, равным сумме моментов инерции всех материальных точек составляющих тело - сумме произведений масс этих точек на квадрат расстояния до оси :

[4]

При вращательном движении используют величину момента силы f относительно данной оси вращения:

[5]

где - плечо силы (кратчайшее расстояние от линии действия силы до оси вращения). В зависимости от направления вращения, создаваемой силой, величине момента приписывается знак плюс или минус (в соответствии с правилом правого винта). Если к телу одновременно приложены моменты нескольких сил, то они складываются, с учетом знака.

Основной закон динамики вращательного движения (аналог второго закона Ньютона) связывает результирующий момент сил , действующих на тело и его угловое ускорение :

[6]

где J – момент инерции тела, относительно оси вращения [4]. Кинетическая энергии вращающегося тела:

[7]

Сложное движение.

Оказывается, что любое движение твердого тела мо­жет быть представлено как наложение двух указанных выше основных видов движения, при этом полная механическая энергия тела равна:

[8]

В замкнутой консервативной системе тел (при отсутствии потерь на преодоление сил сопротивления и трение) сумма их полных механических энергий [8] сохраняется (закон сохранения полной механической энергии консервативной системы тел).

Если замкнутая система тел не является консервативной, то часть этой энергии переходит в немеханическую форму (тепловую, энергию излучения), но остается в системе. В этом случае будет сохраняться сумма полной механической и всех других форм энергии тел вместе взятых (закон сохранения энергии замкнутой системы тел). Разность запаса потенциальной и полной кинетической энергий позволяет определить величину работы, совершенной системой против сил сопротивления.

Описание установки и расчетные формулы

Общий вид установки, используемой в настоящей работе, представлен на рис. 1. Маятник Максвелла представляет собой металлический диск 1, в середине которого укреплен стержень 2. К концам этого стержня прикреплены две крепкие (капроновые) нити 3. Они наматываются на стержень (от концов его к диску). Фиксация диска маятника осуществляется при помощи электромагнита, входящего в устройство регулировки исходного положения 5. Фотодатчик 4 служит для остановки таймера. Диск маятника представляет собой непосредственно сам диск и сменные кольца 6, закрепляющиеся на диске.

При освобождении маятника он начинает движение: поступательное вниз и вращательное вокруг своей оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нитей на стержень, а, следовательно, и к подъему маятника. В верхней точке, маятник останавливается и снова начинает свое движение вниз и т.д. Ход маятника (расстояние, проходимое маятником) может быть измерено по вертикальной рейке с делениями, укрепленной на стойке.

Уравнения движения маятника без учета сил трения имеют вид:

[9]

где m – масса маятника, J – момент инерции маятника, g - ускорение силы тяжести, r – радиус стержня, Т – сила натяжения каждой нити, а – ускорение поступательного движения центра масс маятника, e – угловое ускорение маятника.

Решение системы уравнений [9] позволяет рассчитать теоретическое ускорение поступательного движения центра масс маятника:

[10]

С другой стороны, ускорение , можно определить по измеренному времени движения 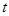и расстоянию , проходимому маятником:

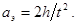[11]

Масса маятника является суммой масс его частей (оси m₀, диска m_д и кольца m_к):

т = m₀ + m_д + m_к. [12]

Момент инерции маятника J , также определяется суммой моментов инерции его частей ( – моменты инерции оси, диска и кольца маятника):

[13]

где r – радиус оси, т₀ = 0,019 кг – масса оси, – радиус диска, m_д = 0,1 кг – масса диска, R_к – внешний радиус кольца, m_к – масса кольца.

Зная линейное ускорение , легко найти скорость движения оси маятника и угловую скорость его вращения, для любого момента времени :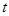

и [14]

Полная кинетическая энергия маятника складывается из энергии поступательного перемещения центра масс (совпадающего с центром оси) и из энергии вращения маятника вокруг оси:

[15]

Интервал надежности

Интервал надежности экспериментального значения ускорения маятника [11], можно рассчитать по правилу расчета погрешности косвенных измерений:

, где [16]

где - коэффициент Стьюдента, зависящий от выбора доверительной вероятности p и числа измерений n.