
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение. Законы сохранения импульса и энергии в механике
Законы сохранения импульса и энергии в механике
Импульсом теланазывается вектор, равный произведению массы тела на его скорость движения, в данной системе отсчета:
 . [1]
. [1]
Работой совершаемая силой  при перемещении тела из точки 1 в точку 2, называется скалярная величина, равная:
при перемещении тела из точки 1 в точку 2, называется скалярная величина, равная:
 [2]
[2]
где  - угол между векторами силы
- угол между векторами силы  и перемещения
и перемещения  .
.
Энергия (возможность совершить работу), запасенная движущимся телом, называется его кинетической энергией:
 [4]
[4]
Энергия, определяемая взаимным расположением взаимодействующих тел или частей одного тела, называется его потенциальной энергией.
В поле тяготения Земли потенциальная энергия тела массой 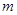 , на высоте
, на высоте  , относительно поверхности Земли:
, относительно поверхности Земли:  .
.
Потенциальная энергия сжатой (растянутой) на величину  пружины, с коэффициентом упругости
пружины, с коэффициентом упругости  :
:  .
.
Механической системой называется совокупность материальных точек (тел), рассматриваемых как единое целое. Система 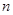 тел называется изолированной (замкнутой), если тела, входящие в нее, взаимодействуют только между собой и не взаимодействуют с другими телами не входящими в нее.
тел называется изолированной (замкнутой), если тела, входящие в нее, взаимодействуют только между собой и не взаимодействуют с другими телами не входящими в нее.
Для описания системы 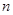 материальных точек (тел) в некоторой системе отсчета, вводится понятие радиус-вектора
материальных точек (тел) в некоторой системе отсчета, вводится понятие радиус-вектора 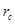 центра масс (центра инерции) системы:
центра масс (центра инерции) системы:

 [2]
[2]
где 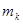 и
и  масса и радиус-вектор
масса и радиус-вектор  - того тела системы,
- того тела системы, 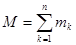 - сумма масс всех тел, входящих в систему. Найдем скорость центра масс системы:
- сумма масс всех тел, входящих в систему. Найдем скорость центра масс системы:
 [3]
[3]
где 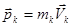 импульс
импульс  - того тела системы,
- того тела системы, 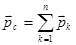 - векторная сумма импульсов всех тел, входящих в систему. Согласно второму закону Ньютона ускорение центра масс (при скоростях движения тел много меньше скорости света
- векторная сумма импульсов всех тел, входящих в систему. Согласно второму закону Ньютона ускорение центра масс (при скоростях движения тел много меньше скорости света 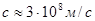 ) равно:
) равно:
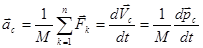 [4]
[4]
где  - векторная сумма всех внешних
- векторная сумма всех внешних  и внутренних
и внутренних  сил, действующих на тела системы. По третьему закону Ньютона векторная сумма всех внутренних сил взаимодействия тел системы между собой будет равна нулю, поэтому:
сил, действующих на тела системы. По третьему закону Ньютона векторная сумма всех внутренних сил взаимодействия тел системы между собой будет равна нулю, поэтому:
 [5]
[5]
Таким образом, поступательное движение системы 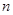 тел, можно описать как движение центра масс системы, под действием векторной суммы внешних сил.
тел, можно описать как движение центра масс системы, под действием векторной суммы внешних сил.
В замкнутой системе векторная сумма всех внешних сил равна нулю  , тогда векторная сумма импульсов тел сохраняется– закон сохранения импульса:
, тогда векторная сумма импульсов тел сохраняется– закон сохранения импульса:
 [6]
[6]
Отметим, что импульс остается постоянным и для незамкнутой системы при условии, что внешние силы в сумме дают нуль. В случае, когда сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление есть нуль, сохраняется составляющая импульса в этом направлении.
Полная механическая энергия системы 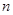 тел, в поле тяготения Земли, может быть представлено как сумма кинетических энергий поступательного движения всех тел системы
тел, в поле тяготения Земли, может быть представлено как сумма кинетических энергий поступательного движения всех тел системы 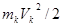 и их потенциальных энергий взаимодействия с Землей
и их потенциальных энергий взаимодействия с Землей 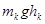 :
:
 [7]
[7]
где  -расстояние по вертикали
-расстояние по вертикали  - того тела от точки, потенциальная энергия, которой принята равной нулю (например – точка на поверхности Земли).
- того тела от точки, потенциальная энергия, которой принята равной нулю (например – точка на поверхности Земли).
В замкнутой консервативной системе (при отсутствии потерь на преодоление сил сопротивления) сумма их полных механических энергий [7] сохраняется - закон сохранения полной механической энергии.
Соударение тел
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением их температуры. Существует два предельных вида удара: абсолютно упругий и абсолютно неупругий.
Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, модуль и направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы тел.
Абсолютно неупругий удар характеризуется тем, что кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается: имеет место закон сохранения суммарной энергии различных видов — механической и внутренней.
Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центры инерции.
Описание установки и расчетные формулы
Схема лабораторной установки показана на рис. 1. К штативу 1 прикреплены два шара. Углы отклонения подвесов от вертикали определяются по шкалам 3. Электромагнит 4 служит для удержания одного из шаров в отклоненном положении.

Рассмотрим пример соударения шаров, приведенный на рис. 2. Отведем один из шаров (например, левый) на некоторый угол a1 и отпустим без начальной скорости. Отклоненный шар будет двигаться, вниз разгоняясь, при этом его потенциальная энергия будет переходить в кинетическую.
Пусть столкновение со вторым шаром происходит в тот момент, когда нить первого шара становится вертикально. По закону сохранения механической энергии:
 [8]
[8]
где т1 – масса шара, g – ускорение свободного падения, h – высота шара в отведенном положении относительно нижней точки траектории, V1 – скорость первого шара в нижней точке перед соударением со вторым.
Из рисунка 2 видно, что
 [9]
[9]
где  – расстояние от точки подвеса до центра тяжести шара,
– расстояние от точки подвеса до центра тяжести шара,  – угол начального отклонения нити. Подставляя [9] в [8] и преобразуя уравнение, найдем выражение для скорости через угол начального отклонения:
– угол начального отклонения нити. Подставляя [9] в [8] и преобразуя уравнение, найдем выражение для скорости через угол начального отклонения:
 [10]
[10]
Массы шаров подобраны так, чтобы после удара они разлетелись в разные стороны. После удара шары получают скорости 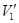 и
и  , и, разлетаясь, отклоняют нити на максимальные углы
, и, разлетаясь, отклоняют нити на максимальные углы 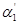 и
и 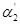 соответственно. Аналогично соотношению [10] получаем:
соответственно. Аналогично соотношению [10] получаем:
 и
и  [11]
[11]
Если удар происходит достаточно быстро, так, что нити во время удара не успевают отклониться на заметный угол, то в направлении горизонтальной оси х выполняется закон сохранения импульса в проекции на эту ось:
 [12]
[12]
При ударе шаров, близком к абсолютно упругому удару, должен также выполняться закон сохранения полной механической энергии:
 [13]
[13]
При абсолютно неупругом ударе шаров полная механическая энергия не сохраняется и выполняется только закон сохранения импульса. Зная скорость движения шара 1 до удара  и, скорость соединившихся шаров 1 и 2 после неупругого удара
и, скорость соединившихся шаров 1 и 2 после неупругого удара  , можно найти энергию, перешедшую из кинетической в другие формы (тепловую и потенциальную энергию деформации шаров):
, можно найти энергию, перешедшую из кинетической в другие формы (тепловую и потенциальную энергию деформации шаров):
 [14]
[14]
Если известна длительность удара t, то из второго закона Ньютона по изменению импульса одного из шаров (например, левого) можно определить среднюю силу взаимодействия между шарами:
 [15]
[15]
Примечание: В формулах [12] - [15], учтено, что скорость  .
.
Дата добавления: 2014-10-31; просмотров: 365; Мы поможем в написании вашей работы!; Нарушение авторских прав |