Описание поведения системы.

Диаграммы последовательностей, деятельности и состояний Концептуальная модель характеризует статические свойства разрабатываемого программного обеспечения. Для описания особенностей его поведения, т. е. возможных действий системы, целесообразно использовать диаграммы последовательностей системы, системные события, системные операции, диаграммы

деятельности, а при необходимости и диаграммы состояний объектов.

Диаграмма последовательностей системы (sequence diagram)

Диаграмма последовательностей системы — графическая модель, которая для определенного сценария варианта использования показывает динамику взаимодействия объектов во времени

[1, 48].

Для построения диаграммы последовательностей системы необходимо:

• идентифицировать каждое действующее лицо (объект) и изобразить для него линию жизни. Крайним слева на диаграмме изображается объект, который является инициатором взаимодействия (см. объект 1 на рис. 3.42). Правее изображается другой объект, который непосредственно

взаимодействует с первым, и т. д.;

• из описания варианта использования определить множество системных событий и их последовательность;

• изобразить системные события в виде линий со стрелкой на конце между линиями жизни действующих лиц и системы, а также указать имена событий и списки передаваемых

значений.

На диаграмме последовательности изображаются только те объекты, которые непосредственно участвуют во взаимодействии, и не показываются возможные статические ассоциации с

другими объектами. При этом диаграмма последовательности имеет как бы два измерения. Одно — слева направо в виде вертикальных линий, каждая из которых изображает линию жизни

отдельного объекта, участвующего во взаимодействии.

Графически каждый объект изображается прямоугольником и располагается в верхней части своей линии жизни (рис. 3.42). Внутри прямоугольника записываются имя объекта и имя класса,

разделенные двоеточием. При этом вся запись подчеркивается, что является признаком объекта, который представляет собой экземпляр класса.

Линия жизни объекта Линия жизни объекта (object lifeline) служит для обозначения

периода времени, в течение которого объект существует в системе и, следовательно, может потенциально участвовать во всех ее взаимодействиях. На диаграмме линия жизни изображается

пунктирной вертикальной линией, ассоциированной с единственным объектом. Если объект существует в системе постоянно, то и его линия жизни должна продолжаться по всей плоскости

диаграммы последовательности от самой верхней ее части до самой нижней (объекты 1 и 2 на рис. 3.42).

Если объекты разрушаются в какой-то момент для освобождения ресурсов системы, то их линия жизни обрывается в момент уничтожения. Для обозначения такого момента в языке

UML используется специальный символ в форме латинской буквы «X» (объект 3 на рис. 3.42). Ниже этого символа пунктирная линия не изображается, поскольку соответствующего объекта в

системе уже нет и этот объект должен быть исключен из всех последующих взаимодействий.

Фокус управления

Объекты на диаграмме последовательности могут находиться в двух состояниях, активном — непосредственно выполняя какие-либо действия, и пассивном, ожидая сообщения от других

объектов. Чтобы явно выделить подобную активность объектов, в языке UML применяется специальное понятие, получившее название фокуса управления (focus of control). Фокус управления

изображается в форме вытянутого узкого прямоугольника (см. объект 1 на рис. 3.42), верхняя сторона которого обозначает начало получения фокуса управления объекта (начало активности),

а ее нижняя сторона — окончание фокуса управления (окончание активности).

Сообщения

Как уже было сказано, диаграмма последовательности описывает динамику взаимодействий между множеством объектов.

Каждое взаимодействие описывается совокупностью сообщений, которыми участвующие в нем объекты обмениваются между собой.

Сообщение (message) представляет собой законченный фрагмент информации, который отправляется одним объектом другому.

Объект, принявший сообщение, должен отреагировать на него какой-либо последовательностью действий, направленных на решение поставленной задачи.

Графически сообщения изображаются горизонтальными стрелками, соединяющими линии жизни или фокусы управления двух объектов на диаграмме последовательности (рис. 3.42).

На рис 3.43 можно увидеть пример построения диаграммы последовательности для моделирования процесса телефонного разговора с использованием обычной телефонной сети.

Объектами в этом примере являются: два абонента а и b, два телефонных аппарата, коммутатор и сам разговор как объект моделирования.

Диаграммы деятельностей (activity diagram)

Для моделирования процесса выполнения операций в языке UML используются так называемые диаграммы деятельности. На этапе анализа требований и уточнения спецификаций

диаграммы деятельностей позволяют конкретизировать основные функции разрабатываемого программного обеспечения.

Состояние действия

Под деятельностью в данном случае понимают задачу (операцию), которую необходимо выполнить вручную или с помощью средств автоматизации. Каждому варианту использования соответствует своя последовательность задач. В теоретическом плане диаграммы деятельности являются обобщенным представлением алгоритма, реализующего анализируемый вариант использования. Графически состояние действия представляется прямоугольником со скругленными углами (рис. 3.44). Внутри этой фигуры записывается выражение действия (action-expression),

которое должно быть уникальным в пределах одной диаграммы деятельности.

Действие может быть записано на естественном языке, некотором псевдокоде или языке программирования. Рекомендуется в качестве имени простого действия использовать глагол с

пояснительными словами (рис. 3.44, а). Если это возможно, то допускается запись действия на том языке программирования, на котором предполагается реализовывать конкретный проект (рис. 3.44, б).

Каждая диаграмма деятельности должна иметь единственное начальное и единственное конечное состояния (рис. 3.45). Саму диаграмму деятельности принято располагать таким образом, чтобы действия следовали сверху вниз. В этом случае начальное состояние будет изображаться в верхней части диаграммы, а конечное — в ее нижней части.

Переходы

При построении диаграммы деятельности используются только нетриггерные переходы, т. е. такие, которые срабатывают сразу после завершения деятельности или выполнения соответствующего действия. Этот переход переводит деятельность в последующее состояние сразу, как только закончится действие в предыдущем состоянии. На диаграмме такой переход изображается сплошной линией со стрелкой.

Если из состояния действия выходит единственный переход, то он может быть никак не помечен. Если последовательно выполняемая деятельность должна разделиться на альтернативные

ветви в зависимости от значения некоторого промежуточного результата (такая ситуация получила название ветвления, а для ее обозначения применяется специальный символ), то таких

переходов несколько и сработать может только один из них.

Именно в этом случае для каждого из таких переходов должно быть явно записано условие в квадратных скобках. При этом для всех выходящих из некоторого состояния переходов должно

выполняться требование истинности только одного из них. Графически ветвление на диаграмме деятельности обозначается небольшим ромбом, внутри которого нет никакого текста

(рис. 3.46). В этот ромб может входить только одна стрелка от того состояния действия, после выполнения которого поток

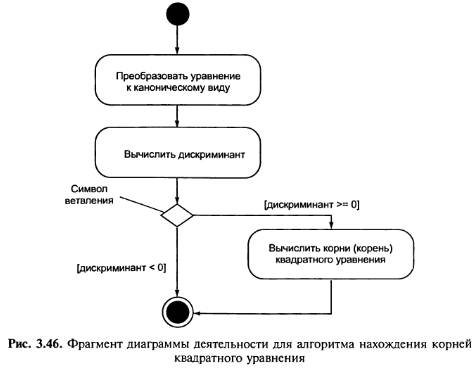
управления должен быть продолжен по одной из взаимно исключающих ветвей. Принято входящую стрелку присоединять к верхней или левой вершине символа ветвления. Выходящих стрелок может быть две или более, но для каждой из них явно указывается соответствующее условие перехода в форме булевского выражения.

На рис. 3.46 представлен фрагмент известного алгоритма нахождения корней квадратного уравнения. В общем случае после приведения уравнения второй степени к каноническому виду

а х х + b x+ с = О в случае отрицательного дискриминанта уравнение не имеет решения на множестве действительных чисел, и дальнейшие вычисления должны быть прекращены. При

неотрицательном дискриминанте уравнение имеет решение, корни которого могут быть получены на основе конкретной расчетной формулы.

Для представления параллельных процессов в языке UML используется специальный символ разделения и слияния параллельных вычислений или потоков управления. Таким символом

является прямая черточка, которая изображается отрезком горизонтальной линии, толщина ее несколько шире основных сплошных линий диаграммы деятельности. При этом разделение

(concurrent fork) имеет один входящий переход и несколько выходящих (рис. 3.47, а). Слияние (concurrent join), наоборот, имеет несколько входящих переходов и один выходящий (рис. 3.47, б).

Диаграммы состояний (statechart diagram)

Главное предназначение этой диаграммы — описать возможные последовательности состояний и переходов, которые в совокупности характеризуют поведение элемента модели в течение

его жизненного цикла. Диаграммы состояний используются для моделирования динамических аспектов системы. По большей части под этим подразумевается моделирование поведения реактивных объектов. Реактивным называется объект, поведение которого лучше всего характеризуется его реакцией на события, произошедшие вне его собственного контекста. У реактивного объекта есть четко выраженный жизненный цикл, когда текущее поведение обусловлено прошлым. Если внешние действия, изменяющие состояния системы, инициируются в произвольные случайные моменты времени, то говорят об асинхронном поведении модели.

Представьте себе моделирование поведения встроенной системы безопасности у себя дома. Она работает непрерывно, реагируя на внешние события, скажем, на разбитое окно. Порядок

событий изменяет поведение системы. Например, обнаружение разбитого окна вызовет срабатывание сигнализации, только если система предварительно была активизирована. Поведение такой системы лучше всего описывается путем моделирования ее устойчивых состояний (например, Ожидание, Активна, Проверка и т. д.), событий, инициирующих смену состояния, и действий, выполняемых при каждой такой смене.