Примеры построения эпюры продольных сил

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).

Делим брус на участки нагружения. Участком нагружения считают часть бруса между внешними силами. На представленном рисунке 3 участка нагружения. Воспользуемся методом течений и определим вну­тренние силовые факторы внутри каждого участка. Расчет начинаем со свободного конца бруса, что­бы не определять величины реакций

Рис.

в опорах.

Участок 1: ΣF_z = 0; - 3F + N₁ = 0; N₁ = 3F. Продольная сила положи­тельна, участок 1 растянут.

Участок 2: ΣF_z = 0; -3F + 2F + N₂ = 0; N₂ = = F. Продольная сила по­ложительна, участок 2 рас­тянут.

Участок 3: ΣF_z = 0; -3F + 2F + 5F - N₃ = 0; N₃ = 4F. Про­дольная сила отрицательна, участок 3 сжат. Полученное значение Nз равно реакции в заделке.

Под схемой бруса строим эпюру продольной силы (рис. 20.26).

Рис.

Эпюрой продольной си­лы называется график рас­пределения продольной си­лы вдоль оси бруса. Ось эпюры параллель­на продольной оси. Нулевая линия прово­дится тонкой линией. Зна­чения сил откладывают от оси, положительные - вверх, отрицательные - вниз. В пределах одного участка значение силы не меняется, поэто­му

эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.

На эпюре проставляются значения N_z. Величины продольных сил откладывают в заранее выбранном масштабе.

Эпюра по контуру обводится толстой линией и заштриховыва­ется поперек оси.

Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.

Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.

Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.

Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.

Напряжения при растяжении и сжатии

При растяжении и сжатии в сечении действует только нормаль­ное напряжение.

Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.

Таким образом, направление и знак напряжения в сечении со­впадают с направлением и знаком силы в сечении (рис. 20.3).

Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. По­этому напряжение можно рассчитать по формуле

Рис.	, где Nz — продольная сила в сечении; А — площадь поперечного сечения. Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна, площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).

Размерность (единица измерения) напряжений — Н/м² (Па), од-
жако это слишком малая единица, и практически напряжения рассчитывают в Н/мм² (МПа): 1 МПа = 10⁶ Па = 1 Н/мм².

При определении напряже­ний брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, ж учитывают места изменений площади поперечных сечений.

Рис.

Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра продольных сил.

Рис.

Рассмотрим брус, нагру­женный внешними силами вдоль оси (рис. 20.5). Обнаруживаем три уча­стка нагружения и определя­ем величины продольных сил. Участок 1: N1 = 0. Внутренние продольные силы равны нулю. Участок 2: N2 = 2F. Про­дольная сила на участке поло­жительна. Участок 3: N3 = 2F - 3F = - F. Продольная сила на участке отрицательна. Брус — ступенчатый. С учетом изменений ве­личин площади поперечного сечения участков напряжений больше.

; (н/мм², МПа)

, =20*10³/ 2*300= 3,33МПа

= 20*10³/ 300=6,66 МПа

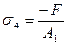=-10*10³/300=-3,33 МПа

Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.