Предельная абсолютная погрешность

Во многих случаях можно определить верхнюю границу модуля точной ошибки.

Определение. Назовем предельной абсолютной погрешностью 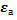приближенного числа а наименьшее положительное число, содержащее одну-две значащих цифры, которое больше или равно модулю точной ошибки, т.е.

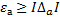(2.4)

Если известна предельная абсолютная погрешность, то для точного значения А можно записать очевидные неравенства:

а - 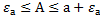(2.5)

Определение. Если приближенное число записано в десятичной системе счисления, то по общепринятому соглашению предельная абсолютная погрешность принимается равной единице последнего знака, если число получено без округления и половине единице последнего знака, если число получено с округлением.

Последним знаком считается первый справа. Это соглашение используется не только в случае , когда приближенное число получено в результате измерения, но и в случае, когда оно получается в результате вычисления и у него отбрасываются несколько знаков справа.

Например – обращение простой дроби в десятичную с сохранением определенного числа знаков после запятой:

а =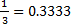

Если достаточно иметь только два знака, то 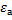=0.01 и можно утверждать, что

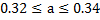
Определение. Предельной относительной погрешностью 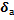приближенного числа а называется отношение его предельной абсолютной погрешности 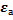к модулю числа а, т.е.

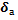= (2.6)

Величину 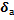обычно выражают в процентах. Например, для мы округлили число p = 3.14, то по принятому нами правилу = , =

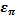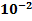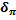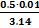
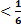
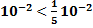
За предельную относительную погрешность примем 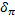= 2 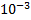= 0.2%

Величину 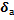выражают еще в промилле - одна тысячная доля или 0.1%