Абсолютная и относительная погрешность вычисления функции одной переменной . Погрешность функции нескольких переменных

Важной проблемой при проведении вычислений с использованием приближенных чисел является вопрос о влиянии погрешности исходных данных (аргумента) на погрешность полученного результата (функции). Для начала рассмотрим случай вычисления функции одного аргумента, который является приближенным числом.

Пусть 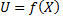, где f(X) непрерывная дифференцируемая функция. Если вместо точного значения аргумента A подставить его приближенное значение а, то полученное значение функции f(a) будет приближенным числом. Найдем выражение для предельной абсолютной погрешности функции .

Определение. Абсолютная погрешность функции равна произведению абсолютной погрешности аргумента на абсолютную величину производной:

=

Предельная относительная погрешность функции:

= =

где δ_а - предельная относительная погрешность аргумента.

Рассмотрим погрешности простейших элементарных функций.

1. Функции u = sin a и u = cos a

Если u = sin a , то = |cos a|* . отсюда видно, что

Аналогично если u = cos a , то = |sin a|* .

Пример. u = sin 15° 25' , а погрешность угла 1’ . Эта погрешность приводит к погрешности 0.001 в синусе. Значит, в качестве 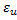можно взять ошибку 0.001.

Функции u = tg a и u = ctg a

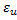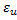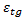Для тангенса = * , а для котангенса = * , то есть ³ и ³ и погрешность зависит от значения угла.