Сложение. За предельную абсолютную погрешность суммы можно принять сумму предельных абсолютных погрешностей слагаемых.

Если u = a + b,

то = + (3.6)

= (3.7)

Или в общем виде предельная абсолютная погрешность суммы:

,где к =1,2,3,…. ,n (3.8)

Вычитание. Вычитание можно представит алгебраическим сложением. Поэтому можно воспользоваться результатом, полученным в процедуре сложения.

Если u = a - b,

то = +

= (3.9)

Умножение. Пусть u=a×b.

Предельная абсолютная погрешность произведения двух сомножителей:

= +b (3.11)

Эту формулу можно распространить на любое число сомножителей.

Относительная погрешность произведения равна сумме относительных погрешностей отдельных сомножителей:

= = =

И в общем виде = (3.12)

Деление.Пусть u =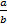

Предельная абсолютная погрешность деления двух чисел:

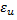= (3.15)

Предельная относительная погрешность деления будет:

= = + (3.16)

Возведение в степень.Пусть u = aⁿ , где n – целое положительное число.

Предельная абсолютная погрешность возведения в степень:

= n*a^n-1 (3.17)

Предельная относительная погрешность n-ой степени в n раз больше предельной относительной погрешности возвышаемого в степень числа.

= n* (3.18)

Извлечение корня. U =

Предельная абсолютная погрешность извлечения корня:

U = , = (3.19)

Предельная относительная погрешность корня n-ой степени в n раз меньше предельной относительной погрешности подкоренного числа.

δ_u=(1/n)·δ_a (3.20)

Сводная таблица формул

Функциональная Предельная абсолютная Предельная относительная

зависимость погрешность погрешность

u = a+b +

u = a-b +

u = a*b *a +

u = +

u = n* n* =n*da

* *da

u=ln a *

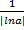Приближенные числа в геодезии получают, как правило, из измерений;

считается, что записанное приближенное число ошибочно не более, чем на половину единицы последнего разряда: то есть число 2.145 - ошибочно на 0.0005 ,

2145 - ошибочно на 0.5 и т.д.