Класс точности средств измерений

Точность средства измерений (точность) – характеристика качества средства измерений, отражающая близость его погрешности к нулю.

Считается, что чем меньше погрешность, тем точнее средство измерений.

Класс точности средств измерений (класс точности) – обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Пределы допускаемых основной и дополнительных погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей.

Пределы допускаемой основной погрешности устанавливают в последовательности, приведенной в ГОСТ 8.401-80 «Классы точности средств измерений».

Нормируемые метрологические характеристики типа средства измерений (нормируемые метрологические характеристики) – совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативными документами на средства измерений.

Пределы допускаемой абсолютной основной погрешности устанавливают по формуле:

(2.1)

или

, (2.2)

где Δ– пределы допускаемой абсолютной погрешности, выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы;

Х – значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;

a, b – положительные числа, не зависящие от Х.

В обоснованных случаях пределы допускаемой абсолютной погрешности могут устанавливаться по более сложной формуле или в виде графика либо таблицы.

Пределы допускаемой приведенной основной погрешности устанавливают по формуле:

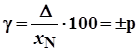, (2.3)

где γ – пределы допускаемой приведенной основной погрешности, %;

Δ – пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (2.1);

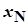– нормирующее значение, выраженное в тех же единицах, что и Δ;

р – отвлеченное положительное число, выбираемое из ряда 1·10 ; 1,5·10 ; 2·10 ; 2,5·10 ; 4·10 ; 5·10 ; 6·10 (n = 1, 0, -1, -2 и т. д.).

Пределы допускаемой относительной погрешности устанавливают по формуле

, (2.4)

если Δ установлено по формуле (2.1),

или по формуле

, (2.5)

где δ – пределы допускаемой относительной основной погрешности, %;

q – отвлеченное положительное число, выбираемое из ряда, приведенного выше;

– больший (по модулю) из пределов измерений;

с, d – положительные числа, выбираемые из ряда, приведенного выше, причем

;

.

В обоснованных случаях пределы допускаемой относительной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.

Пределы допускаемых дополнительных погрешностей устанавливают:

– в виде постоянного значения для всей рабочей области влияющей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;

– путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

– путем указания зависимости предела допускаемой дополнительной погрешности от влияющей величины (предельной функции влияния);

– путем указания функциональной зависимости пределов допускаемых отклонений от номинальной функции влияния.

Пределы допускаемой дополнительной погрешности, как правило, устанавливают в виде дольного (кратного) значения предела допускаемой основной погрешности.

Класс точности, как обобщенная характеристика, обозначается либо в документации, либо на средствах измерения.

Если в документации, то, например, класс точности 0,02/0,01 означает назначение предела допускаемой основной погрешности по формуле (2.5) при с = 0,02 и d = 0,01:

.

Если на средстве измерения, то возможны следующие варианты.

1,5 – предел допускаемой основной погрешности назначен по формуле 2.3 (если нормирующее значение выражено в единицах величины на входе (выходе) средства измерений).

1,5 – по формуле 2.3 (если нормирующее значение принято равным длине шкалы или ее части).

– по формуле 2.4.

М – по формуле 2.1 и 2.2.

С – по формуле 2.2.