Исключение случайных погрешностей

Мы убедились, что результат измерения – случайная величина. В связи с этим при проведении любых измерений наряду с получением числа, выраженного в определенных единицах (результата измерений х), необходимо определить степень достоверности результата измерения.

Количественно оценить степень достоверности результата измерения – означает получение количественной меры близости между случайным результатом измерения х и неизвестным (но не случайным) истинным значением Х измеряемой величины.

Из теории вероятностей известно, что случайные величины исчерпывающе описываются законами распределения. Обычно – дифференциальным законом распределения (плотность распределения вероятностей) f(Δ).

Одним из наиболее распространенных законов распределения случайной погрешности является нормальный закон распределения

, (2.6)

где .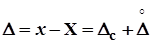

Из 2.6 видно, что нормальный закон распределения целиком определяется двумя параметрами – и σ. В теории вероятности принято называть математическим ожиданием случайной величины Δ, а в метрологии – систематической погрешностью (когда Δ – абсолютная погрешность). В теории вероятностей σ принято называть дисперсией случайной величины Δ, а в метрологии эта величина является мерой разброса погрешности вокруг Δ_с.

Величины и σ имеют размерность погрешности Δ и поэтому удобны в качестве ее характеристики.

Вид нормального закона распределения представлен на рис. 2.5.

Рис. 2.5. Нормальный закон распределения погрешностей

Из 2.5 следует, что 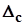лежит на оси симметрии кривой f(Δ), то есть систематическую погрешность можно рассматривать как среднее значение погрешностей, которые получаются при многократных измерениях одного и того же размера физической величины. Поэтому систематическую погрешность считают величиной постоянной. Из 2.5 также следует, что чем больше σ, тем кривая f(Δ) более полога и имеет меньший максимум, то есть чем больше σ, тем более вероятны значительные отклонения погрешностей от их среднего значения .

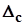При нормальном законе распределения погрешностей вероятность того, что погрешность отдельного измерения превысит по абсолютной величине 3σ, составляет 0,003 (0,3%). Такой вероятностью на практике пренебрегают и называют величину 3σ максимально возможной погрешностью («закон трех сигм»).

Если величине 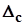известна и исключена из результата измерения, то это эквивалентно переносу начала координат на рис.2.5 в точку 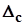. В этом случае математическое ожидание погрешности Δ, составляющей которой теперь является только случайная составляющая 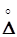, будет равно нулю (рис 2.5 преобразуется в рис 2.6).

Рис.2.6. Нормальный закон распределения погрешностей при Δ_с = 0

Исключить случайную погрешность 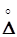из результата однократного измерения нельзя, так как неизвестно, какое конкретное значение примет 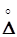. Однако можно существенно уменьшить влияние 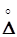на результат измерения, проводя многократные измерения одного и того же размера физической величины и усредняя их результаты. Иными словами, для исключения случайной погрешности 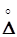из результата измерения необходимо определить его математическое ожидание, которое и будет истинным значением измеряемой величины Х.

В этом случае с учетом того, что , плотность распределения результатов однократных измерений будет подчиняться также нормальному закону:

,

где σ – дисперсия результатов однократных измерений, равная дисперсии погрешности.