Прямое многократное измерение

Многократное измерение – измерение физической величины одного и того же размера, результат которого получается из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений.

При рассмотрении многократных измерений вводят понятие наблюдения. Под наблюдением понимают однократное измерение размера физической величины.

Результаты наблюдений при прямых равноточных измерениях, выполненных с использованием одинаковых по точности средств измерений в одних и тех же условиях с одинаковой тщательностью, равновероятны, то есть вероятности их появления

.

При математической обработке результатов наблюдений многократного измерения выполняют следующие операции:

1. Исключают известные систематические погрешности 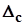из результатов наблюдений, то есть определяются исправленные результаты наблюдений.

2. Вычисляют среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерения:

,

где n – конечное число наблюдений.

Среднее арифметическое и будет оценкой математического ожидания ряда наблюдений. Оценкой, а не математическим ожиданием, т.к. n конечно, относительно рассеиваются результаты отдельных наблюдений. Если 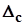= 0, то будет действительным значением измеряемой величины и при будет стремиться к истинному значению измеряемой величины Х.

3. Вычисляется среднее квадратическое отклонение результата наблюдения. С этой целью определяют отклонение результата каждого наблюдения от среднего арифметического (по величине и знаку)

,

где – i -я остаточная погрешность (случайное отклонение i-го результата наблюдения от действительного значения измеряемой величины).

Остаточные погрешности обладают свойством (при ):

.

Это свойство позволяет проверить правильность вычисления остаточных погрешностей.

В итоге по сумме квадратов всех остаточных погрешностей определяют среднеквадратическое отклонение результата наблюдения (средняя квадратическая погрешность результата наблюдения):

. (2.7)

Это оценка дисперсии однократного измерения – σ.

Значение S с достаточным приближением можно определить по формуле:

где и – минимальное и максимальное значение результатов наблюдений, упорядоченных по возрастающим значениям в вариационный ряд .

4. Если значения или 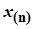резко отличаются от других членов вариационного ряда (промах), т.е. не подчиняются нормальному закону распределения, то его отбрасывают и в обработке результатов наблюдений не учитывают.

При числе наблюдений принадлежность к нормальному закону распределения не проверяют, т.к. считают, что появление промаха при малом числе наблюдений маловероятно.

5. При конечном (ограниченном) числе наблюдений n значение , принимаемое нами за действительное значение измеряемой величины, ещё остается случайной величиной, которая имеет свою дисперсию – . Из теории вероятности известно, что дисперсия (дисперсия результата серии наблюдений) связана с дисперсией однократного измерения σ соотношением

.

Тогда оценкой дисперсии при ограниченном числе наблюдений будет:

,

или с учетом выражения 2.7

.

Здесь – среднеквадратичное отклонение результата серии наблюдений, то есть средняя квадратическая погрешность результата многократного измерения.

Из выражения для следует, что, увеличивая n, если это возможно, случайную составляющую погрешности многократного измерения можно сделать пренебрежимо малой по сравнению с систематической. Такой прием называется фильтрацией случайной составляющей погрешности измерения.

Рассмотренные выше числовые характеристики называют точечными оценками, так как выражаются они одним числом (точкой на числовой оси). Это приближенные оценки математического ожидания и дисперсий из-за отсутствия полной информации о законах распределения погрешностей (ограниченности числа n наблюдений). Более полным являются интервальные оценки погрешностей.

6. Вычисляют доверительные границы случайной погрешности результата многократного измерения – доверительный интервал:

.

В этот интервал попадает истинное значение Х измеряемой величины с заданной вероятностью Р:

.

Чем больше величина доверительного интервала, тем с большей надежностью Р искомая величина Х попадает в этот интервал.

Доверительные границы ε случайной погрешности результата многократного измерения находят по формуле

,

где t – коэффициент Стьюдента, который зависит от доверительной вероятности P и числа наблюдений n.

7. Запись результата многократного измерения осуществляется в виде:

, (2.8)

где – среднее арифметическое результатов наблюдений (действительное значение измеряемой величины Х);

Δ – абсолютная погрешность измерения;

Р – доверительная вероятность.

Как правило, .

Определив Δ по приведенным выше выражениям, можно записать результат многократного измерения согласно выражения 2.8, принимая во внимание, что числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение Δ. Число значащих цифр при записи Δ должно быть не более двух.