Область определения функции, в которой есть дробь

Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.

Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:

Пример 1

Найти область определения функции

Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:

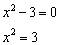
Полученное уравнение имеет два корня: . Данные значения не входят в область определения функции. Действительно, подставьте или в функцию и вы увидите, что знаменатель обращается в ноль.

Ответ: область определения:

Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений ». Значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:

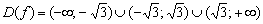
Кому как нравится.

В точках функция терпит бесконечные разрывы, а прямые, заданные уравнениями являются вертикальными асимптотами для графика данной функции. Впрочем, это уже немного другая тема, и далее я на этом не буду особо заострять внимание.

Пример 2

Найти область определения функции

Задание, по существу, устное и многие из вас практически сразу найдут область определения. Ответ в конце урока.

Всегда ли дробь будет «нехорошей»? Нет. Например, функция определена на всей числовой оси. Какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен: . Таким образом, область определения данной функции: .

Рекомендую запомнить, при любом значении «икс» и положительной константе:

Все функции наподобие определены и непрерывны на .

Чуть более сложнА ситуация, когда знаменатель оккупировал квадратный трёхчлен:

Пример 3

Найти область определения функции

Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:

Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.

Ответ: область определения:

Пример 4

Найти область определения функции

Это пример для самостоятельного решения. Решение и ответ в конце урока. Советую не лениться с простыми задачками, поскольку к дальнейшим примерам накопится недопонимание.